Copyright © 2001 Elsevier Science B.V. All rights reserved.
Journal of Marine Systems
Volume 29, Issues 1-4 , May 2001, Pages 141-155
Lagrangian statistics in the central North Pacific
Rick Lumpkina, b
and Pierre Flamenta, b
a University of Hawaii at Manoa, Honolulu, HI, USA
b IFREMER, Plouzané, France
Received 6 December 1999; accepted 3 June 2000.
Abstract
Lagrangian integral scales, diffusivities, dispersion and velocity spectra
are calculated using surface drifter trajectories in the central North Pacific.
The meridional integral time scale is relatively homogeneous throughout the
region; a large increase in the zonal time and length scales south of Hawaii
is attributed to meanders in the North Equatorial Current. Except in this
current, the initial dispersion is consistent with Taylor's Theorem. For
lags of 20–120 days, the meridional dispersion can be modeled by a constant
eddy diffusivity. Shear in the mean zonal currents magnifies the zonal dispersion
at long lags. In the Lagrangian spectra, the energetic eddy band is at 3–20
days west of Hawaii, 10–40 days east and north of Hawaii, and 20–60 days
in the North Equatorial Current. In the wake of Hawaii, energetic lee vortices
produce sharp peaks in the cyclonic and anticyclonic rotary spectra.
Author Keywords: Diffusivities; North Pacific; Eddy

1. Introduction
The gyre-scale motion of the central North Pacific Ocean consists of the
eastward North Pacific Current and the westward North Equatorial Current
(NEC). The Hawaiian Islands lie near the northern extent of the NEC, partially
blocking it. West of the islands, energetic mesoscale lee vortices dominate
the instantaneous currents and have profound effects on the time-averaged
flow field (Patzert; Lumpkin and Flament). Over the last decade, these currents and vortices
have been sampled by WOCE/SVP drifting buoys (Fig. 1).
Single-particle Lagrangian integral scales, which give the dominant stirring
scales of oceanic turbulence, can be calculated from their trajectories. Classical
diffusion theory relates these integral scales to the long-term dispersion
in terms of an eddy diffusivity. However, this parameterization requires
stationary and homogeneous currents, while oceanic drifters experience inhomogeneous
mean currents and a mesoscale field which changes in both space and time.
As a consequence, Freeland et al. (1975)
concluded that even the short-time dispersion of deep, neutrally buoyant floats
cannot be described by classical theory. Subsequent drifter studies (cf.
Colin; Krauss and Paduan)
have not found this inconsistency, although at longer times the dispersion
may not asymptote to the diffusive limit of classical theory.

 (190K)
(190K)
Fig. 1. Top: Spaghetti diagram of 20-day drifter trajectory
segments. Colors give the mean drift direction (legend in upper-right corner).
Bottom: Map of vorticity created from the spectra of 90-day drifter segments.
Blue indicates predominantly cyclonic vorticity, red indicates anticyclonic
vorticity. Black polygons indicate the drifter group subregions. Arrows show
the mean velocity of the drifter group.

In this paper, we present the Lagrangian statistics of surface drifters
in the central North Pacific. In Section 2, a brief review
of classical diffusion theory is presented. Section 3
describes the drifter database and integral scale calculations, and presents
these scales for several groups of drifters. In Section 4,
the diffusion model's predictions are compared to the directly observed dispersion
of the drifters. It is shown that the meridional dispersion agrees with classical
theory, but the zonal dispersion is greatly magnified. Section
5 examines the hypothesis that this magnification is due to meridional
shear in the mean zonal currents. The Lagrangian spectra are examined for
significant zonal/meridional and rotary motion in Section
6. Section 7 concludes by examining the relevance
of an empirical law which relates length and time scales to characteristic
eddy speeds.
2. Classical diffusion theory
Consider a cloud of particles released into a fluid at a single point.
The instantaneous current u(t) experienced by a particle can
be divided into a mean component uo (identical for all
particles), and a fluctuating component u'(t) (which may vary
from one particle to the next). The position of an individual particle in
the cloud is x(t)=uot+x'(t),
where
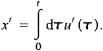
|
(1) |
Dispersion is <x'2>, where the brackets denote
an average over the particle ensemble. Assuming that u' is ergodic,
Eq. (1) can be used to derive Taylor's Theorem (Taylor, 1921):
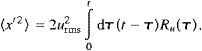
|
(2) |
where
urms
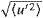
and the autocorrelation function
Ru is
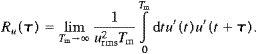
|
(3) |
The characteristic time scale of dispersion is the Lagrangian integral
time
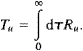
|
(4) |
It can be combined with the eddy speed urms to derive the Lagrangian integral
length Lu=urmsTu.
At short times, Ru 1 and the dispersion is
1 and the dispersion is
<x'2> urms2t2 (t<<Tu)
(ballistic regime).
urms2t2 (t<<Tu)
(ballistic regime). |
(5) |
In this short-time limit, the rms particle displacement increases linearly
with time, with a slope equal to the rms eddy speed. At large times,
<x'2> 2urms2Tut (t>>Tu)
(random-walk regime),
2urms2Tut (t>>Tu)
(random-walk regime), |
(6) |
assuming that the integral in
Eq. (4) converges.
The rms particle displacement slows from the initial rate (
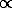 t
t) to a random-walk (
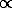
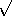 t
t).
By analogy with Fickian diffusion, dispersion can be parameterized as
an eddy diffusivity Kxx (Taylor;
Batchelor and Davis):
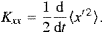
|
(7) |
From
Eq. (6), the diffusivity asymptotes
to
in the random walk regime
t>>
Tu
(again, assuming homogeneity and stationarity for
u').
3. Integral scales in the central North Pacific
A total of 356 WOCE/SVP surface drifters have been deployed in or passed
through the central North Pacific (10–30°N, 140–180°W). Raw satellite
fixes of drifter position were quality-checked using a two-step scheme and
interpolated to 1/4-day intervals via kriging (Hansen and Poulain, 1996). The interpolated data span
286 drifter-years (Fig. 1). West of the Hawaiian Islands,
many cycloidal trajectories are created by drifters orbiting westward- propagating
lee vortices. This westward motion is visible on either side of 19.5°N
along 155–170°W. At 19.5°N, a narrow band of eastward drift (colored
green in Fig. 1) marks the Hawaiian Lee Countercurrent
(Lumpkin, 1998). South of the islands, the mean westward
NEC dominates the trajectories, which also display zonally extended meridional
fluctuations. East and north of the islands, the trajectories are a mix of
loops and wiggles with no visually discernible mean drift.
After formation immediately west of Hawaii, lee vortices drift westward
due to the 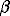 -effect and advection by the North Equatorial Current. Because anticyclonic
eddies tend to drift southward while cyclonic eddies drift northward (Chassignet and Cushman-Roisin, 1991),
the overall field of lee eddies is not random; instead, it is organized in
a pattern superficially resembling a Kármán vortex street (Lumpkin, 1998). Rectification of this field may produce
the elongated, counter-rotating lee gyres which extend for over 1000 km west
of the islands in the time-averaged currents (Lumpkin
and Flament). The vorticity structure of this geophysical-scale
wake can be seen by breaking the drifter trajectories into 90-day nonoverlapping
segments, calculating the mean rotary spectra in 3×1° cells, and
integrating the spectra over subinertial frequencies to obtain the cyclonic
and anticyclonic variance. Fig. 1 shows the resulting
map of cyclonic/total variance, scaled from +1 (purely cyclonic) to -1 (purely
anticyclonic). In the lee gyres, as much as 70% of the variance is of one
sign; the division between the cyclonic and anticyclonic gyre is at 19.5°N,
the latitude of the eastward Hawaiian Lee Countercurrent.
-effect and advection by the North Equatorial Current. Because anticyclonic
eddies tend to drift southward while cyclonic eddies drift northward (Chassignet and Cushman-Roisin, 1991),
the overall field of lee eddies is not random; instead, it is organized in
a pattern superficially resembling a Kármán vortex street (Lumpkin, 1998). Rectification of this field may produce
the elongated, counter-rotating lee gyres which extend for over 1000 km west
of the islands in the time-averaged currents (Lumpkin
and Flament). The vorticity structure of this geophysical-scale
wake can be seen by breaking the drifter trajectories into 90-day nonoverlapping
segments, calculating the mean rotary spectra in 3×1° cells, and
integrating the spectra over subinertial frequencies to obtain the cyclonic
and anticyclonic variance. Fig. 1 shows the resulting
map of cyclonic/total variance, scaled from +1 (purely cyclonic) to -1 (purely
anticyclonic). In the lee gyres, as much as 70% of the variance is of one
sign; the division between the cyclonic and anticyclonic gyre is at 19.5°N,
the latitude of the eastward Hawaiian Lee Countercurrent.
In order to calculate Lagrangian statistics for the various dynamically
homogeneous regions, the 90-day trajectory segments were organized into six
groups according to their median latitude and longitude (Fig.
1). For each segment within a group, the ensemble-averaged velocity was
removed from the drifter-derived velocities. Because direct estimates of
the autocorrelation function R are contaminated by noise and uncertainties
in the mean current, and this contamination dominates R at large lags,
the integration in Eq. (4) was truncated at the first
zero crossing of R (cf. (Freeland; Krauss and Poulain)).
The mean scales of the six groups are shown in Fig. 2
and listed in Table 1. The lee gyres and northwest groups
have the highest eddy kinetic energy levels, while the North Equatorial Current
and northeast groups have the lowest. The rms eddy speeds for all groups
except the cyclonic gyre are significantly anisotropic, with zonal speeds
exceeding meridional speeds by a factor of 1.1–1.4. In the cyclonic gyre,
where the maximum eddy kinetic energy levels are found, the ratio is not
significantly different from unity. For the five groups north of the North
Equatorial Current, the time scales are quite homogeneous, with an overall
mean of (Tu, Tv)=(6.3±0.5,
4.6±0.2) days. The smallest time scales are in the cyclonic gyre,
where drifters advect rapidly around lee vortices. The overall mean length
scale of these five groups is (Lu, Lv)=(68±3,
46±3) km. Perhaps the most striking feature of Fig.
2 is the much larger zonal time and length scales in the North Equatorial
Current. These large scales suggest that low-frequency, zonally extended
meanders (rather than more isotropic, higher-frequency mesoscale vortices)
dominate the variability here (Krauss and Böning, 1987).
Eddy diffusivities were calculated using Eq. (8), and
range from 11.9×103 m2/s in the eddy-rich anticyclonic
gyre to 2.3×103 m2/s in the North Equatorial
Current.

 (85K)
(85K)
Fig. 2. Top: zonal (left) and meridional (right) rms
eddy speed (cm/s). Middle, upper: Lagrangian zonal (left) and meridional
(right) time scales (days). Middle, lower: Lagrangian zonal (left) and meridional
(right) length scales (km). Bottom: Zonal (left) and meridional (right) eddy
diffusivities (103 m2/s).

Table 1. Lagrangian integral scales in each group, calculated
from independent 90-day segments
 (<1K)
(<1K)

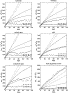
Fig. 3 shows the zonal and meridional scales and diffusivities
as functions of the rms eddy speed. For comparison, data are included from
Colin de Verdière (1983) (eastern North Atlantic,
47°N, 11°W), Krauss and Böning (1987) (central
North Atlantic from 30°N to 55°N), and Poulain and
Niiler (1989) (southern California Current System). Except for the North
Equatorial Current values, the central North Pacific scales are consistent
with the central North Atlantic values for a given rms eddy speed, suggesting
that the underlying Eulerian length and time scales of the mesoscale fluctuations
are similar. The North Equatorial Current group was further south than any
drifters in the North Atlantic study; thus, the discrepancy in Lagrangian
zonal length scales, and the much smaller length scales found by Colin de
Verdière at 47°N, may be caused by an Eulerian length scale which
decreases with increasing latitude (Stammer, 1997). The central North Pacific meridional scales
are also consistent with those in the California Current; the inconsistency
in zonal scales between these studies may be due to the influence of the
North American coast.

 (14K)
(14K)
Fig. 3. Lagrangian properties as a function of rms eddy
speed (left: zonal, right: meridional). Circles with standard error bars
are the central North Pacific values. For comparison, triangles give values
from Krauss and Böning (1987), pluses from Colin de Verdière (1983), and solid lines from Poulain and Niiler (1989) (their least-squares fits to
a cloud of values).

4. Asymptotic behavior of the dispersion
Is the dispersion consistent with Taylor's Theorem? To address this, we
divided the trajectories into 120-day segments and resampled the tracks every
10 days, treating each segment as independent (Freeland
and Poulain). Fig. 4 shows the rms
displacement of the drifter groups, with the ballistic growth rate (Eq. (5) given by the rms eddy speeds. Everywhere except
in the North Equatorial Current, the initial growth is consistent with Taylor's
Theorem. Zonal dispersion in the NEC is faster than ballistic, growing instead
at ~(14.6 cm/s)t.

 (30K)
(30K)
Fig. 4. Dispersion and diffusivity for the six drifter
groups. In all cases, the upper curve is zonal and the lower is meridional.
Solid lines: rms displacement (km). Thin dashed lines: ballistic rms displacement
according to rms eddy speed (km). Dots: eddy diffusivity calculated via Eq. (7) (103 m2/s). Heavy dashed lines:
random-walk diffusivity limit predicted by Eq. (8) (103
m2/s).

If the drifters enter the random-walk regime at long times, the eddy diffusivity
should approach a constant. Fig. 4 shows the diffusivity
calculated via Eq. (7) and low-passed at 15 days, with
heavy dashed lines indicating the limit predicted by Eq. (8).
For all groups, meridional diffusivity reaches the predicted value by day
20, with slight fluctuations thereafter. Taylor's Theorem does not describe
the zonal dispersion of any group. In the cyclonic gyre, drifters disperse
zonally like a random walk in days 15–100, with an apparent diffusivity 1.5
times greater than predicted by the integral scales, but beyond day 100 the
rms displacement resumes linear growth. In contrast, the anticyclonic gyre
group takes much longer to settle into random-walk dispersion (60 days), but
remains random-walk-like to day 120. For all other groups, the zonal dispersion
never acts like a random walk; instead, rms displacement switches from the
linear ballistic rate (except for the NEC group) to a smaller, but still
linear, growth rate through day 120, with the diffusivity according to Eq. (7) continuously increasing.
5. Shear dispersion
The long-time linear growth in zonal rms displacement is consistent with
dispersion driven by shear in the mean zonal currents. To demonstrate this,
consider mean currents of the form
<u>=uo+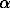 y', <v>=0,
y', <v>=0, |
(9) |
(see Appendix of
Krauss and Böning (1987)).
A spatially homogeneous estimate of <
u> will be averaged over
a meridional scale
B (the maximum meridional size of the tracer cloud).
This estimate, denoted with a hat, is
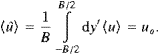
|
(10) |
The estimate of u' is, thus, contaminated by the meridional shear
of the mean current:
û'=u-<û>=uo+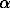 y'+u'-uo=u'+
y'+u'-uo=u'+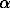 y'.
y'. |
(11) |
<û'2>=<u'2>+2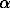 <u'y'>+
<u'y'>+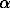 2<y'2>.
2<y'2>. |
(12) |
If u' and y' are uncorrelated,
<û'2>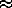 <u'2>+2
<u'2>+2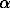 2<v'2>Tvt,
t>>Tv,
2<v'2>Tvt,
t>>Tv, |
(13) |
where
Eq. (6) has been used. Assuming <
u'
2>~
O(<
v'
2>),
<û'2>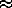 <u'2>,
<u'2>, |
(14) |
for
t<<(
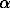 2Tv
2Tv)
-1. This time scale
can be estimated as follows: east of the Hawaiian Islands, the zonal current
is 0 m/s at 26°N and is -0.2 m/s at 14°N, giving |
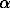
|~1.5×10
-7 s
-1 . Using this value and
Tv~3.2
days, (2
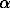 2Tv
2Tv)
-1~930 days. Because
we are interested in dispersion for
t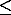
120 days, we proceed under the assumption that
Eq. (14)
applies and restrict this derivation to the time range
Tu<<t<<(2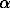 2Tv)-1.
2Tv)-1. |
(15) |
The estimated autocorrelation of u' is
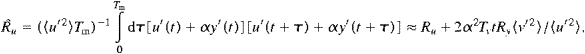
|
(16) |
where
Ry is the autocorrelation of
y'(
t), a function which decays considerably more slowly than
Rv. Because
Ry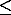
1,
t<<1/2
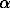 2Tv
2Tv, and <
u'
2>~
O(<
v'
2),
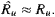
|
(17) |
The estimated autocorrelation function is not significantly contaminated
by the meridional shear in <u>, so the integral scales should
not be either.
The long-time dispersion is
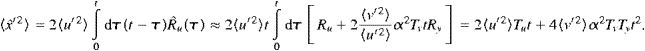
|
(18) |
where
Ty is the integral time scale
of
y' (for all 90-day independent drifter segments in the central
North Pacific, the mean value of
Ty is 11 days).
The second term on the right-hand side of
Eq. (18) scales
to the first term as
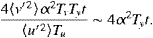
|
(19) |
Thus, for t>1/4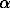 2Ty~100 days, xrms
grows linearly due to the meridional shear of the mean zonal current.
2Ty~100 days, xrms
grows linearly due to the meridional shear of the mean zonal current.
According to Eq. (18), the mean shear scales as
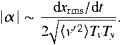
|
(20) |
Thus, an estimate of |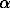 | can be derived from the observed long-time dispersion. From Fig. 4,
| can be derived from the observed long-time dispersion. From Fig. 4,  xrms/
xrms/ t for the east group of drifters between days 100 and 120 is ~0.05
m/s. Using this value, v'~0.11 m/s, Tv~5
days and Ty~11 days, Eq. (20)
gives |
t for the east group of drifters between days 100 and 120 is ~0.05
m/s. Using this value, v'~0.11 m/s, Tv~5
days and Ty~11 days, Eq. (20)
gives |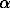 |~3.5×10-7 s-1, approximately twice the direct
measurement (|
|~3.5×10-7 s-1, approximately twice the direct
measurement (|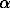 |
|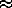 1.5×10-7 s-1). This discrepancy may be due to
the first term in the right-hand side of Eq. (18) playing
a non-negligible role. Nevertheless, given the crude scaling arguments involved,
this order-of-magnitude agreement suggests that the gyre-scale meridional
shear can account for the observed long-time zonal dispersion.
1.5×10-7 s-1). This discrepancy may be due to
the first term in the right-hand side of Eq. (18) playing
a non-negligible role. Nevertheless, given the crude scaling arguments involved,
this order-of-magnitude agreement suggests that the gyre-scale meridional
shear can account for the observed long-time zonal dispersion.
6. Lagrangian spectra
The integral scales presented in this paper are essentially first-moment
descriptions of the Lagrangian velocity spectra. They do not, however, give
details of the cyclonic/anticyclonic distribution of energy or higher-moment
information. In order to examine the mean Lagrangian spectra, we took non-overlapping
120-day segments of the drifter trajectories, removed the mean from the velocity
time series, applied a 10% cosine window and calculated the spectra. Individual
spectra within a group were used to obtain standard error bars for the mean
spectral energy density via bootstrapping.
Fig. 5 shows the variance-preserving spectra of zonal
and meridional drifter speed. In the lee gyre, the energetic eddy-containing
band is at 3–20 days period. This band shifts to 10–40 days for the other
groups north of the North Equatorial Current, and to 20–60 in the NEC. At
the lowest resolved frequencies, the zonal component of velocity is more
energetic than the meridional component for all groups except the northwest
and northeast. Higher-frequency motion (periods smaller than 30–40 days)
are everywhere isotropic. The lee gyre spectra are dominated by sharp peaks;
the rotary spectra (Fig. 6) show that these peaks are
due to single-signed lee vortices. Cyclonic peaks are at 4–6, 8 and 14 days;
anticyclonic peaks are at 6, 12 and 22 days, with additional, barely significant
peaks at 3 and 7 days. The cyclonic spectrum in the anticyclonic gyre has
a peak at 5 days, due to strong lee anticyclones occasionally advecting weaker,
wind-generated cyclones southward in the immediate lee of Hawaii.1 The discretization of
eddy energy suggests that the motion is a resonant response to direct forcing,
or that some process or combination of processes is quantizing the mesoscale
variability within the eddy band (such as vortex generation by shear instability
and downstream vortex merging (Flament et al., 2001)).
For the northwest and northeast groups, anticyclonic energy is significantly
greater than cyclonic energy throughout most of the eddy band. The northwest
spectrum also has a prominent anticyclonic peak at 15 days, possibly due to
eddy generation at the Subtropical Front (Qiu, 1998).

 (35K)
(35K)
Fig. 5. Variance-preserving plots (frequency times energy
density) of the Lagrangian spectra of u (solid, dark shading) and
v (dashed, light shading) for the six groups. Shading indicates
the standard error bars.

 (39K)
(39K)
Fig. 6. Variance-preserving plots (frequency times energy
density) of the Lagrangian cyclonic (solid, dark shading) and anticyclonic
(dashed, light shading) spectra for the six groups. Shading indicates the
standard error bars.

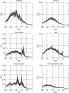
Log–log plots of the spectra for the zonal/meridional components of velocity
are shown in Fig. 7. The spectra of groups north of the
North Equatorial Current and east of the Hawaiian Archipelago have a low-frequency
energy plateau with a cutoff at 20–30 days, followed by a high-frequency
slope of ~-2. A similar Lagrangian spectral slope was found by Colin de Verdière (1983), who attributed it to the
off-resonance mesoscale response to direct wind forcing. In the North Equatorial
Current, the zonal spectrum is red to the lowest resolved frequency. Both
NEC spectra have a shallow slope of ~-1.5 past a cutoff of ~40 days, which
becomes even shallower at 3–6 days before rapidly dropping at very high frequencies.
This weak spectral slope implies that motion at frequencies higher than the
cutoff significantly impact dispersion (Rupolo et al., 1996). The spectra of the lee gyre groups
have a low-frequency cutoff at 40 days, an intermediate slope of ~-1 from
6–40 days, and a much steeper high-frequency slope. A similar intermediate
power-law regime was discovered in neutrally buoyant float spectra by Rupolo et al. (1996), who attributed it to the presence
of coherent vortices driving anomalous dispersion over the initial 10 integral
time scales. The log–log rotary spectra (Fig. 8) show
that the intermediate regime exists only in the spectra of one sign: the dominant
vorticity of that lee gyre. The opposite-signed spectra have a -2 slope,
similar to those east of Hawaii. Lee vortices create an intermediate slope
of ~-3/4, with a dropoff steeper than -3 past the high-frequency cutoff.

 (38K)
(38K)
Fig. 7. Log–log plots of the Lagrangian spectra of u
(solid, heavy shading) and v (dashed, light shading) for the six groups.
Shading indicates the standard error bars.

 (41K)
(41K)
Fig. 8. Log–log plots of the Lagrangian cyclonic (solid,
heavy shading) and anticyclonic (dashed, light shading) spectra for the six
groups. The shading indicates the standard error bars.

7. Discussion
Is there a universal empirical law independently relating the length and
time scales of eddies to their velocity variance? If so, maps of eddy diffusivity
could be constructed directly from maps of eddy kinetic energy (Böning, 1988). Two models have
been proposed for this law. Observations of SOFAR floats (700 and 1300 m
depth) deployed in MODE and LDE suggest that the Lagrangian scales are related
by (Price, in (Rossby and McWilliams)):
| Lu=urmsTu,
Kxx=urms2Tu,
Tu constant. |
(21) |
| Tu=Lu/urms,
Kxx=urmsLu,
Lu constant, |
(22) |
in a study of surface North Atlantic drifters;
Brink et al. (1991) found the same
relationship applied to drifters in the California Coastal Transition Zone.
As noted by
Davis (1991), both the
length and time scales may change with changing EKE: a tendency for observations
to behave more like
(21) and
(22)
depends on the relative fluctuation of
Lu and
Tu.
Drifter studies in the California Current system (
Poulain
and
Swenson) have found complementary
changes in the two scales with varying
urms such that neither
of the two laws is statistically superior. As demonstrated in
Fig. 3, the central North Pacific data behave similarly.
The zonal length scales are inconsistent with the constant time scale model
(
Eq. (21), and both zonal and meridional time scales
decrease with increasing eddy speed. However, the meridional length scale
increases significantly with eddy speed. Neither model is statistically superior
for describing variations in zonal diffusivity as a function of eddy speed.
The meridional diffusivity can be matched by the constant time scale model
(
Eq. (21) within the error bars, while the constant length
scale model (
Eq. (22) cannot.
Within the North Equatorial Current, zonally stretched, highly anisotropic
meanders set the dominant scales of oceanic stirring. Higher-frequency, more
isotropic eddies determine these scales to the north. In the oceanic wake
of the islands, highly energetic and coherent lee vortices magnify the EKE
levels and diffusivities, and create relatively narrow peaks in the rotary
spectra. Except in the North Equatorial Current, dispersion is initially
ballistic. Over at least 120 days, the meridional dispersion remains consistent
with Taylor's Theorem, changing from ballistic to random-walk dispersion
which can be characterized by a constant eddy diffusivity set by the integral
scales and rms eddy speed. The meridional dispersion, thus, does not appear
to be inhibited by conservation of planetary vorticity (O'Dwyer et al., 2000), which should be anticipated when
rms meridional displacement has reached
Zonal dispersion is considerably faster than meridional dispersion, and
is not consistent with Taylor's Theorem for a homogeneous flow in the long-time
random-walk limit. This is an ubiquitous result in open-ocean drifter studies,
attributed to topographic effects (Rossby
and Freeland), spatial anisotropy of meanders (Colin and Krauss), the 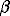 -effect (Haidvogel and Keffer, 1984),
and meridional shear in the mean zonal flow (Krauss and
Böning, 1987). The final hypothesis is consistent with the observed
shear of the North Pacific Subtropical Gyre. Zonal eddy diffusivities constructed
from the integral scales do not represent an asymptotic limit to the observed
growth rate of dispersion.
-effect (Haidvogel and Keffer, 1984),
and meridional shear in the mean zonal flow (Krauss and
Böning, 1987). The final hypothesis is consistent with the observed
shear of the North Pacific Subtropical Gyre. Zonal eddy diffusivities constructed
from the integral scales do not represent an asymptotic limit to the observed
growth rate of dispersion.
Calculating eddy diffusivities has become a tradition in drifter studies,
and in some circumstances the diffusion model may indeed describe the dispersion
of passive tracers. In the presence of a red cascade of eddy energy, however,
such diffusivities can be a misleading way of closing the momentum equations.
For example, an explicit calculation of Reynolds stress in the wake of the
Hawaiian Islands reveals an eddy-to-mean eastward momentum flux convergence
at the latitude of the Hawaiian Lee Countercurrent (19–20°N) (Lumpkin, 1998). Given the presence of such a "negative
eddy diffusivity," we advise the reader to approach traditionally computed
eddy diffusivities, such as the ones presented here, with caution!

Acknowledgements
We thank Capt. Brainard and the crew of the R.V. Townsend Cromwell, Guy
and Dominique of the yacht Touaou, and Pierre and Minouche of the yacht Meranda
for their help deploying the drifters. We thank other investigators whose
drifters, initially deployed of California or in the equatorial Pacific,
eventually reached our area. They generously made the data available through
the WOCE and TOGA databases. J. Firing, S. Kennan, M. Pazos, M. Sawyer, C.
Lumpkin and D. Young assisted with data collection and processing. This work
was supported by the United States Office of Naval Research (Grant #N000149710147),
the National Atmospheric and Oceanographic Administration (Joint Institute
for Marine and Atmospheric Research, Grant #NA67RJ0154) and our host institutions.
Contribution number 5077 of the School of Ocean and Earth Science and Technology,
and JIMAR contribution number 00-333.

References
Batchelor, 1949G.K. Batchelor
, Diffusion in a field of homogeneous turbulence: I. Eulerian analysis. Aust.
J. Sci. Res., Ser. A 2 (1949), pp. 437–450
Böning, 1988C. Böning
, Characteristics of particle dispersion in the North Atlantic: an alternative
interpretation of SOFAR float results. Deep-Sea Res. 35
(1988), pp. 1379–1385.
Brink et al., 1991K.H. Brink, R.C.
Beardsley, P.P. Niiler, M. Abbott, A. Huyer, S. Ramp, T. Stanton and D. Stuart
, Statistical properties of near-surface flow in the California coastal transition
zone. J. Geophys. Res. 96 (1991), pp. 14693–14706.
Chassignet and Cushman-Roisin, 1991E.P.
Chassignet and B. Cushman-Roisin , On the influence of a lower layer on the
propagation of nonlinear oceanic eddies. J. Phys. Oceanogr. 21
(1991), pp. 939–957.
Colin de Verdière, 1983A.
Colin de Verdière , Lagrangian eddy statistics from surface drifters
in the eastern North Atlantic. J. Mar. Res. 41 (1983),
pp. 375–398.
Davis, 1982R. Davis , On relating
Eulerian and Lagrangian velocity statistics: single particles in homogeneous
flows. J. Fluid Mech. 114 (1982), pp. 1–26.
Davis, 1991R.E. Davis , Observing
the general circulation with floats. Deep-Sea Res. 38
(1991), pp. S531–S571.
Flament et al., 2001P. Flament,
R. Lumpkin, J. Tournadre and L. Armi , Vortex pairing in an unstable anticyclonic
shear flow: discrete subharmonics of one pendulum day. J. Fluid Mech.
(2001) submitted for publication .
Freeland et al., 1975H.J. Freeland,
P.B. Rhines and T. Rossby , Statistical observations of the trajectories of
neutrally buoyant floats in the North Atlantic. J. Mar. Res. 33
(1975), pp. 383–404.
Haidvogel and Keffer, 1984D.B.
Haidvogel and T. Keffer , Tracer dispersal by mid-ocean eddies. Dyn. Atmos.
Oceans 8 (1984), pp. 1–40.
Hansen and Poulain, 1996D.V.
Hansen and P.-M. Poulain , Quality control and interpolations of WOCE–TOGA
drifter data. J. Atmos. Oceanogr. Tech. 13 (1996),
pp. 900–909.
Krauss and Böning, 1987W.
Krauss and C.W. Böning , Lagrangian properties of eddy fields in the
northern North Atlantic as deduced from satellite-tracked buoys. J. Mar.
Res. 45 (1987), pp. 259–291.
Lumpkin, 1998Lumpkin, C., 1998.
Eddies and Currents of the Hawaiian Islands. PhD dissertation, School of
Ocean and Earth Sciences and Technology, University of Hawaii at Manoa.
McWilliams et al., 1983J. McWilliams,
E. Brown, H. Bryden, C. Ebbesmeyer, B. Elliot, R. Heinmiller, B.L. Hua, K.
Leaman, E. Lindstrom, J. Luyten, S. McDowell, W.B. Owens, H. Perkins, J.
Price, L. Regier, S. Riser, H. Rossby, T. Sanford, C. Shien, B. Taft and
J.V. Leer , The local dynamics of eddies in the western North Atlantic. In:
A. Robinson, Editor, Eddies in Marine Science, Springer-Verlag, Berlin
(1983), pp. 92–113.
O'Dwyer et al., 2000J. O'Dwyer,
R.G. Williams, J.H. LaCasce and K.G. Speer , Does the potential vorticity
distribution constrain the spreading of floats in the North Atlantic?. J.
Phys. Oceanogr. 30 (2000), pp. 721–732.
Paduan and Niiler, 1993J.D. Paduan
and P.P. Niiler , Structure of velocity and temperature in the northeast Pacific
as measured with Lagrangian drifters in Fall 1987. J. Phys. Oceanogr.
23 (1993), pp. 585–600.
Patzert, 1969Patzert, W.C., 1969.
Eddies in Hawaiian waters. Technical Report 69-8, Hawaiian Institute of Geophysics,
University of Hawaii at Manoa.
Poulain and Niiler, 1989P.-M.
Poulain and P.P. Niiler , Statistical analysis of the surface circulation
in the California current system using satellite-tracked drifters. J.
Phys. Oceanogr. 19 (1989), pp. 1588–1603.
Qiu, 1998B. Qiu , Seasonal eddy
field modulation of the North Pacific Subtropical Countercurrent: TOPEX/POSEIDON
observations and theory. J. Phys. Oceanogr. 29 (1998),
pp. 2471–2486.
Rossby et al., 1975T. Rossby,
A.D. Voorhis and D. Webb , A quasi-Lagrangian study of mid-ocean variability
using long range SOFAR floats. J. Mar. Res. 33 (1975),
pp. 355–382.
Rossby et al., 1983H.T. Rossby,
S.C. Riser and A.J. Mariano , The western North Atlantic––a Lagrangian viewpoint.
In: A. Robinson, Editor, Eddies in Marine Science, Springer-Verlag,
Berlin (1983).
Rupolo et al., 1996V. Rupolo,
B.L. Hua, A. Provenzale and V. Artale , Lagrangian velocity spectra at 700
m in the western North Atlantic. J. Phys. Oceanogr. 26
(1996), pp. 1591–1607.
Stammer, 1997D. Stammer , Global
characteristics of ocean variability estimated from regional TOPEX/POSEIDON
altimeter measurements. J. Phys. Oceanogr. 27 (1997),
pp. 1743–1769.
Swenson and Niiler, 1996M.S.
Swenson and P.P. Niiler , Statistical analysis of the surface circulation
of the California Current. J. Geophys. Res. 101 (1996),
pp. 22631–22645.
Taylor, 1921G.I. Taylor , Diffusion
by continuous movements. Proc. London Math. Soc. 20
(1921), pp. 196–212.

1 This process has
been observed using a synthesis of the drifter trajectories, AVHRR imagery
and satellite altimetry by Lumpkin (1998).
![]()

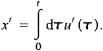
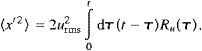

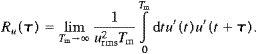
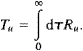
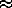 1 and the dispersion is
1 and the dispersion is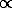 t) to a random-walk (
t) to a random-walk (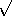 t).
t).
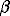 -effect and advection by the North Equatorial Current. Because anticyclonic
eddies tend to drift southward while cyclonic eddies drift northward
-effect and advection by the North Equatorial Current. Because anticyclonic
eddies tend to drift southward while cyclonic eddies drift northward 


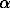 y', <v>=0,
y', <v>=0,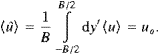
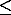 120 days, we proceed under the assumption that
120 days, we proceed under the assumption that 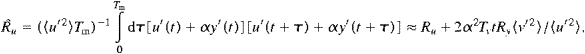
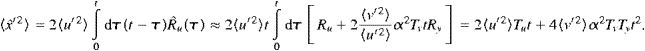
 xrms/
xrms/


