Copyright © 2001 Elsevier Science B.V. All rights reserved.
Progress in Oceanography
Volume 54, 2002, Pages 493-501.
A state variable for characterizing water masses and their diffusive stability:
spiciness
P. Flament
University of Hawaii at Manoa, Honolulu, HI 96822, USA.
1. Introduction
The distributions of potential temperature  and salinity s on surfaces of constant potential density
and salinity s on surfaces of constant potential density 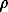 (
( ,s,p=pref) are not independent: displaying
both is redundant. Vertical profiles of either temperature or salinity also
contains some information on the density stratification. It is therefore
natural to introduce a state variable defined to be most sensitive to isopycnal
thermohaline variations, and least correlated with the density field. The
concept of such a variable is not new; it has been used, among many others,
by Stommel (1962) to discuss the
sharpness of the
,s,p=pref) are not independent: displaying
both is redundant. Vertical profiles of either temperature or salinity also
contains some information on the density stratification. It is therefore
natural to introduce a state variable defined to be most sensitive to isopycnal
thermohaline variations, and least correlated with the density field. The
concept of such a variable is not new; it has been used, among many others,
by Stommel (1962) to discuss the
sharpness of the  –s curve in deep water, by Munk (1981)
to separate internal waves from intrusive fine-structure, by Olbers, Wenzel, and Willebrand (1985)
as a tracer in an inverse model of the Atlantic circulation.
–s curve in deep water, by Munk (1981)
to separate internal waves from intrusive fine-structure, by Olbers, Wenzel, and Willebrand (1985)
as a tracer in an inverse model of the Atlantic circulation.
Flament (1986) defined and constructed
such a state variable  (
( ,s) in a way useful to characterize water masses, and also to
indicate double-diffusive stability. Following Munk (1981),
,s) in a way useful to characterize water masses, and also to
indicate double-diffusive stability. Following Munk (1981),
 was called `spiciness', being largest for hot (spicy) and salty water. It
has been widely used to study the California Current System ( Niiler; Lynn; Simpson;
Huyer; Barth and Steger).
A number of papers in the present volume use this definition of spiciness,
which this note makes readily accessible.
was called `spiciness', being largest for hot (spicy) and salty water. It
has been widely used to study the California Current System ( Niiler; Lynn; Simpson;
Huyer; Barth and Steger).
A number of papers in the present volume use this definition of spiciness,
which this note makes readily accessible.
2. Definition
2.1. Spiciness as a state variable
A state variable is associated with a family of isopleths in the  –s plane, intersecting the family of isopycnals. A water type can thus
be defined interchangeably by its (
–s plane, intersecting the family of isopycnals. A water type can thus
be defined interchangeably by its ( ,s) coordinates, or by its (
,s) coordinates, or by its ( ,
, ) coordinates. The definition of spiciness should not depend on a specific
choice of scales on the
) coordinates. The definition of spiciness should not depend on a specific
choice of scales on the  and s axes, and must, therefore, be invariant for all geometric
transforms allowed in the
and s axes, and must, therefore, be invariant for all geometric
transforms allowed in the  –s plane. These consist of changes of scales along the axes; rotations
are not allowed because
–s plane. These consist of changes of scales along the axes; rotations
are not allowed because  and s have different physical dimensions. A scale-invariant constraint
is to require that, at any point, the slopes of the isopycnals and of the
spiciness isopleths are equal and of opposite sign (Fig.
1):
and s have different physical dimensions. A scale-invariant constraint
is to require that, at any point, the slopes of the isopycnals and of the
spiciness isopleths are equal and of opposite sign (Fig.
1):
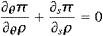
|
(1) |
which defines a unique family of spiciness isopleths, regardless
of the scales chosen for the axes.

 (6K)
(6K)
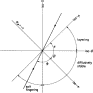
Fig. 1. A point of the  –s plane with the scales chosen so that the isopycnal is at with the
axes. The spiciness isopleth at that point is constructed so that ; it is
orthogonal to the isopycnal with this choice of scales. A vertical profile
unstable to salt fingering is drawn, with
–s plane with the scales chosen so that the isopycnal is at with the
axes. The spiciness isopleth at that point is constructed so that ; it is
orthogonal to the isopycnal with this choice of scales. A vertical profile
unstable to salt fingering is drawn, with 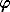 =-71.6°(R
=-71.6°(R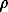 =2); the arrow indicates the downward direction. The sectors corresponding
to profiles diffusely stable, unstable to salt fingering and layering, and
gravitationally unstable are also shown. Positive angles are counter-clockwise.
=2); the arrow indicates the downward direction. The sectors corresponding
to profiles diffusely stable, unstable to salt fingering and layering, and
gravitationally unstable are also shown. Positive angles are counter-clockwise.

Geometrically, at any point the isopycnals and the spiciness isopleths
are symmetric with respect to the  –s directions. When the scales are chosen so that the isopycnals
are inclined at 45° with the axes at a point, the spiciness isopleths
are orthogonal to the isopycnals at that point. Note that (2) is not a total differential, since in general the condition
of integrability
–s directions. When the scales are chosen so that the isopycnals
are inclined at 45° with the axes at a point, the spiciness isopleths
are orthogonal to the isopycnals at that point. Note that (2) is not a total differential, since in general the condition
of integrability
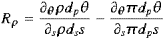
|
(4) |
where
p is the hydrostatic pressure.
Equation
(4) provides a simple physical interpretation of (
2):
the spiciness isopleths are simply the lines along which the density ratio
R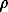
=-1 (the adiabatic temperature gradient
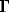
has been neglected in (
4); this is justified in the upper
ocean and the main thermocline, where most water mass interleaving occurs).
The vertical gradients of 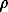 and
and  are:
are:
so that
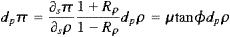
|
(6) |
in which
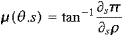
|
(7) |
is an integrating factor of the ordinary differential
Eq. (2), and in which the stability angle
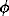
. has been defined such that:
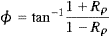
|
(8) |
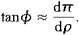
|
(9) |
2.3. Constructing spiciness
Spiciness  is constructed using potential density referenced to the surface pref=0
following Fofonoff (1985). The solution
is expressed as
is constructed using potential density referenced to the surface pref=0
following Fofonoff (1985). The solution
is expressed as
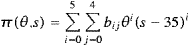
|
(10) |
and the
bij are found by minimizing
the weighted mean square error on (
1) and on
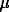
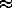
1 :
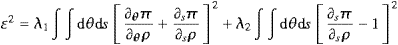
|
(11) |
The integration is carried over the domain delimited by (0.32), (30.35),
(30.38) and (0.35), containing most of the water masses of the oceans (seeWorthington and Levitus). The weights 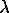 1=0.8 and
1=0.8 and 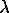 2=0.2 were chosen to emphasize the geometric constraint between
the spiciness isopleths and the isopycnals; the resulting coefficients are
not very sensitive to this choice. The coefficients bij
are given in Table 1; as a convention, b00=0
so that
2=0.2 were chosen to emphasize the geometric constraint between
the spiciness isopleths and the isopycnals; the resulting coefficients are
not very sensitive to this choice. The coefficients bij
are given in Table 1; as a convention, b00=0
so that  (0,35)=0. The families of isopycnals and spiciness isopleths are shown in
Fig. 2.
(0,35)=0. The families of isopycnals and spiciness isopleths are shown in
Fig. 2.

Table 1. Coefficients of the polynomial expansion (10).
In the last column, (k) means .10k. (coefficient, c- and
matlab programs available at http://satftp.soest.hawaii.edu/spice/)
 (<1K)
(<1K)

 (15K)
(15K)
Fig. 2. The families of isopycnals (dashed) and spiciness
isopleths (solid) with the reference pressure at the surface. With the scales
chosen for this graph, the lines are orthogonal at about 8.5 °C. The
domain over which the error (11) was minimized is delimited
by dotted lines.

The rms and maximum errors on (1) are 2×10-3
and 5×10-3, and the rms and maximum errors on 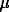
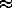 1 are 1.4×10-2 and 4×10-2 respectively,
the maximum values being confined to the edges of the integration domain.
For the critical cases of the stability limits
1 are 1.4×10-2 and 4×10-2 respectively,
the maximum values being confined to the edges of the integration domain.
For the critical cases of the stability limits 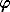 =±45°, the corresponding rms and maximum errors on
=±45°, the corresponding rms and maximum errors on 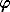 are 0.4° and 1.2° are negligible for practical purposes.
are 0.4° and 1.2° are negligible for practical purposes.
3. Example
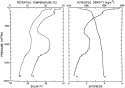
Fig. 3 shows a profile through a Mediterranean water
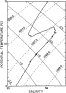
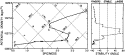
eddy (`salt lens'), south of the Azores (Armi & Zenk, 1984). The corresponding  –s curve is shown in Fig. 4. Fig. 5a shows the profile of spiciness using potential
density as the ordinate. The isotherms and isohalines are overlaid. In this
representation, they are approximately at ±45° with the
–s curve is shown in Fig. 4. Fig. 5a shows the profile of spiciness using potential
density as the ordinate. The isotherms and isohalines are overlaid. In this
representation, they are approximately at ±45° with the 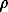 –
– axes, and indicate the limits of diffusive stability: a segment of the
profile steeper than an isotherm or an isohaline is diffusely stable. Fig. 5b shows the corresponding stability angle profile,
computed over vertical intervals larger than the scale of the fine-structure
observed below the salt lens.
axes, and indicate the limits of diffusive stability: a segment of the
profile steeper than an isotherm or an isohaline is diffusely stable. Fig. 5b shows the corresponding stability angle profile,
computed over vertical intervals larger than the scale of the fine-structure
observed below the salt lens.

 (10K)
(10K)
Fig. 3. Vertical profiles through a Mediterranean salt
lens, using pressure as the ordinate, taken on 17 September 1984 at 31°42'N;
22°00'W (courtesy of L. Armi). (a) salinity and potential temperature
(referenced to the surface), (b) potential density and spiciness.

 (12K)
(12K)
Fig. 4.  –s curve for the profile shown in Fig. 3.
The isopycnals and isospices are overlaid.
–s curve for the profile shown in Fig. 3.
The isopycnals and isospices are overlaid.

 (16K)
(16K)
Fig. 5. (a) profile of spiciness using potential density
as the ordinate; the profile is diffusely stable where the slope is steeper
than the isotherms and isohalines, indicated by dashed lines. (b) corresponding
profile for the stability angle 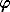 , computed by a least-square fit over 50 m intervals.
, computed by a least-square fit over 50 m intervals.

The main thermocline, from A to B, is slightly diffusively unstable to
salt-fingering, with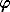 ~-72°(R
~-72°(R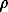 ~2). A small diffusively-stable section BC is followed by the top of
the salt lens CD, unstable to layering, with
~2). A small diffusively-stable section BC is followed by the top of
the salt lens CD, unstable to layering, with 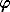 ~-72°(R
~-72°(R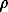 ~0.5). The core of the lens DE is diffusively stable. Below the lens,
there is a region strongly unstable to salt-fingering, with
~0.5). The core of the lens DE is diffusively stable. Below the lens,
there is a region strongly unstable to salt-fingering, with 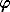 ~-84°(R
~-84°(R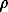 ~1.25), associated with conspicuous thermohaline inversions and staircase-like
structures.
~1.25), associated with conspicuous thermohaline inversions and staircase-like
structures.
In Fig. 5a, the stability angle is simply the angle
between the tangent to the curve and the vertical (cf. Fig.
1 rotated 45° clockwise). This representation has thus the advantage
of displaying the stability regime graphically, without the need to explicitly
compute scale-dependent derivatives as in Fig. 5b.
4. Discussion
Analogous variables were proposed by Veronis and Jackett.
Veronis (1972) constrained the isopleths of his variable
 V (
V ( ,s) to be orthogonal to the isopycnals in the
,s) to be orthogonal to the isopycnals in the  –s plane. However his definition depends on the scaling of the axes:
geometric orthogonality is lost when the scales are altered, i.e. his constraint
is invariant for rotations, but not for scale changes, which should be required
for a state variable.
–s plane. However his definition depends on the scaling of the axes:
geometric orthogonality is lost when the scales are altered, i.e. his constraint
is invariant for rotations, but not for scale changes, which should be required
for a state variable.
The variable  JMD introduced by Jackett and McDougall (1985)
differs from
JMD introduced by Jackett and McDougall (1985)
differs from  in three important aspects. Firstly, they enforce the constraint (1) exactly on a single spiciness isopleth, instead
of in a least square sense over the domain of ocean water masses. Secondly,
they require that, along all isopycnals, d
in three important aspects. Firstly, they enforce the constraint (1) exactly on a single spiciness isopleth, instead
of in a least square sense over the domain of ocean water masses. Secondly,
they require that, along all isopycnals, d JMD=2
JMD=2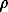 -1
-1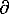 s
s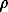 ds; although this is also related to double-diffusive convection (i.e.
Ruddick & Turner, 1979), Eq. (9) provides a more transparent interpretation in terms
of diffusive stability, with direct applications ( Ruddick,
1983). Thirdly,
ds; although this is also related to double-diffusive convection (i.e.
Ruddick & Turner, 1979), Eq. (9) provides a more transparent interpretation in terms
of diffusive stability, with direct applications ( Ruddick,
1983). Thirdly,  JMD is dimensionless, whereas
JMD is dimensionless, whereas  has the same physical dimensions as density, yielding simple and elegant
expressions for ((6), (7) and (9)). For practical purposes and over the range of oceanic
water masses, linear conversions between
has the same physical dimensions as density, yielding simple and elegant
expressions for ((6), (7) and (9)). For practical purposes and over the range of oceanic
water masses, linear conversions between  JMD and
JMD and  can be obtained by:
can be obtained by:
 JMD=0.97
JMD=0.97 +23.8
+23.8 |
(12a) |
and
 =1.03
=1.03 JMD-24.5
JMD-24.5 |
(12b) |
with standard errors less than 0.025 in units of either

or
 JMD.
JMD.
5. Conclusions
Spiciness, as defined here, is ideally suited for the combined description
of interleaving and double-diffusive processes at the boundary between different
water masses, such as, for example, shelf-slope and coastal upwelling fronts,
or marginal seas outflows. It has the practical advantage of lumping together
the concept of a state variable decoupled from density, and the concept of
an indicator of diffusive stability.
The 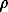 –
– plane has an elegant geometrical property: isotherms and isohalines
are approximately straight lines, the non-linearity of the equation of state
being nearly entirely contained in their variable spacing. In other words,
with properly engraved non-linear rulers for
plane has an elegant geometrical property: isotherms and isohalines
are approximately straight lines, the non-linearity of the equation of state
being nearly entirely contained in their variable spacing. In other words,
with properly engraved non-linear rulers for  and for s, a
and for s, a  –s diagram could be constructed entirely by hand, without recourse
to a calculator or to special pre- printed isopycnal paper.
–s diagram could be constructed entirely by hand, without recourse
to a calculator or to special pre- printed isopycnal paper.
A word of caution: spiciness, just like potential density, is only useful
over limited vertical excursions near the pressure to which they are referenced;
for large vertical ranges, the slope of the isopycnals and spiciness isopleths
vary significantly with pressure, and generalization of the polynomial expansion
to include a reference pressure dependence is needed. The maximum pressure-induced
slope error for spiciness between the surface and 1000 m depth, amounts to
1.5° at  =20 and s=35, and 3° at
=20 and s=35, and 3° at  =10 and s=35.
=10 and s=35.

Acknowledgements
The author would like to thank an anonymous referee for his thorough review,
which helped clarify an earlier version of this note. This work was supported
by the Office of Naval Research. Contribution number 5323 of the School of
Ocean and Earth Science and Technology.

References
Armi and Zenk, 1984. L. Armi and
W. Zenk , Large lenses of highly saline Mediterranean water. Journal of
Physical Oceanography 14 (1984), pp. 1560–1576.
Barth, Pierce and Smith, 2000. J.A.
Barth, S.D. Pierce and R.L. Smith , A separating coastal upwelling jet at
Cape Blanco, Oregon and its connection to the California Current System. Deep-Sea
Research 1 47 (2000), pp. 783–810.
Flament, 1986. Flament, P. (1986).
Finestructure and subduction associated with upwelling filaments.
PhD dissertation, University of California San Diego.
Fofonoff, 1985. N.P. Fofonoff
, Physical properties of seawater: a new salinity scale and equation of state
for sea-water. Journal of Geophysical Research 90
(1985), pp. 3332–3342.
Huyer, Barth, Kosro, Shearman and
Smith, 1998. A. Huyer, J.A. Barth, P.M. Kosro, R.K. Shearman and R.L.
Smith , Upper-ocean water mass characteristics of the California current,
summer 1993. Deep-Sea Research I 45 (1998), pp. 1411–1442.
Levitus, 1982. Levitus, S. (1982).
Climatological atlas of the world ocean. NOAA Professional Paper,
13, 1-173. Rockville, MD.
Lynn and Simpson, 1990. R.J. Lynn
and J.J. Simpson , The flow of the undercurrent over the continental borderland
off southern California. Journal of Geophysical Research 95
(1990), pp. 12995–13008.
Munk, 1981. W. Munk , Internal
waves and small-scale processes. In: Evolution of physical oceanography,
MIT Press, Cambridge, MA (1981), pp. 264–291.
Niiler, Poulain and Haury, 1989.
P.P. Niiler, P.M. Poulain and L.R. Haury , Synoptic three-dimensional
circulation in an onshore-flowing filament of the California Current. Deep-Sea
Research 36 (1989), pp. 385–405.
Olbers, Wenzel and Willebrand, 1985.
D.J. Olbers, M. Wenzel and J. Willebrand , The inference of North Atlantic
circulation patterns from climatological hydrographic data. Reviews of
Geophysics 23 (1985), pp. 313–356.
Ruddick, 1983. B.R. Ruddick
, A practical indicator of the stability of the water column to double-diffusive
activity. Deep-Sea Research 30 (1983), pp. 1105–1107.
Ruddick and Turner, 1979. B.R.
Ruddick and J.S. Turner , The vertical length scale of double-diffusive intrusions.
Deep-Sea Research 26 (1979), pp. 903–913.
Simpson and Lynn, 1990. J.J.
Simpson and R.J. Lynn , A mesoscale eddy dipole in the offshore California
Current. Journal of Geophysical Research 95 (1990),
pp. 13009–13022.
Steger, Schwing, Collins, Rosenfeld,
Garfield and Gezgin, 2000. J.M. Steger, F.B. Schwing, C.A. Collins, L.K.
Rosenfeld, N. Garfield and E. Gezgin , The circulation and water masses in
the Gulf of the Farallones. Deep-Sea Research I 47
(2000), pp. 907–946.
Stommel, 1962. H. Stommel ,
On the cause of the temperature-salinity curve in the ocean. Proceedings
of the National Academy of Science USA 48 (1962), pp.
764–766.
Turner, 1973. J.S. Turner ,
Buoyancy effects in fluids. , Cambridge University Press, Cambridge (1973).
Veronis, 1972. G. Veronis ,
On properties of seawater defined by temperature, salinity and pressure.
Journal of Marine Research 30 (1972), pp. 227–255.
Washburn and Käse, 1987. L.
Washburn and R.H. Käse , Double diffusion and the distribution of the
density ratio in the Mediterranean waterfront southeast of the Azores. Journal
of Physical Oceanography 17 (1987), pp. 12–25.
Worthington, 1981. V. Worthington
, The water masses of the World Ocean: some results of a fine-scale census.
In: Evolution of physical oceanography, MIT Press, Cambridge, MA (1981),
pp. 42–69.

Corresponding author:
Pierre Flament,
Department of Oceanography, School of Ocean and Earth Sciences and Technology,
University of Hawaii at Manoa, 1000 Pope Road, Honolulu, HI 96822, USA.
Tel.: +1-808-956-6663; fax: +1-808-956-9225; email:
pflament@soest.hawaii.edu
 (
( ,s) most sensitive to isopycnal thermohaline variations and least
correlated with the density field is proposed.
,s) most sensitive to isopycnal thermohaline variations and least
correlated with the density field is proposed.  is constructed so that its diapycnal gradient d
is constructed so that its diapycnal gradient d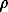
 is related to the density gradient ratio R
is related to the density gradient ratio R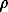 :d
:d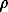

 (1+R
(1+R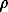 )/(1-R
)/(1-R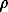 ). It is simultaneously a tracer conserved by isentropic motions, and
an indicator of diffusive stability. It is useful for the combined description
of interleaving and double-diffusive processes at the boundary between water
masses.
). It is simultaneously a tracer conserved by isentropic motions, and
an indicator of diffusive stability. It is useful for the combined description
of interleaving and double-diffusive processes at the boundary between water
masses. ![]()
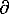

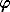 =-71.6°(R
=-71.6°(R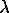 ) along a line
) along a line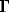 has been neglected in (
has been neglected in (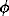 . has been defined such that:
. has been defined such that: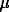




 V (
V (