© Copyright American Meteorological Society 2000
Journal of Physical Oceanography: Vol. 30, No. 1, pp. 233–242.Vortex Merging in a 1˝-Layer Fluid on an f Plane*
Rick Lumpkin and Pierre Flament
School of Ocean and Earth Science and Technology, University of Hawaii, Honolulu, Hawaii, and IFREMER, Plouzané, France
Rudolf Kloosterziel
School of Ocean and Earth Science and Technology, University of Hawaii, Honolulu, Hawaii
Laurence Armi
Scripps Institution of Oceanography, University of California, San Diego, La Jolla, California
(Manuscript received 1 February 1999, 5 August 1999)
ABSTRACT Mass,
angular momentum, and energy budgets are examined in an analytical model
of vortex merging relevant to midlatitude mesoscale eddies. The vortices
are baroclinic and cyclogeostrophic. The fluid surrounding them is assumed
to remain quiescent. It is shown that due to this surrounding fluid, angular
momentum is conserved when expressed in both the inertial and rotating frames
of reference.
Mass,
angular momentum, and energy budgets are examined in an analytical model
of vortex merging relevant to midlatitude mesoscale eddies. The vortices
are baroclinic and cyclogeostrophic. The fluid surrounding them is assumed
to remain quiescent. It is shown that due to this surrounding fluid, angular
momentum is conserved when expressed in both the inertial and rotating frames
of reference.
 Lens-shaped solid-body vortices can conserve mass, angular momentum, and energy when they merge. If an upper-layer of thickness H1 is included in the model, the merged vortex must have either less energy or mass than the sum of the original two vortices.
Lens-shaped solid-body vortices can conserve mass, angular momentum, and energy when they merge. If an upper-layer of thickness H1 is included in the model, the merged vortex must have either less energy or mass than the sum of the original two vortices.
 A
more complex model of the vortex azimuthal structure is then considered,
which includes a constant vorticity shell surrounding the solid-body core.
If the shell is large compared to the core, the mass, angular momentum, and
energy can all be conserved in the merged vortex. However, if the shell is
small, the merged vortex must have less energy or mass than in the solid-body
case.
A
more complex model of the vortex azimuthal structure is then considered,
which includes a constant vorticity shell surrounding the solid-body core.
If the shell is large compared to the core, the mass, angular momentum, and
energy can all be conserved in the merged vortex. However, if the shell is
small, the merged vortex must have less energy or mass than in the solid-body
case.
TABLE OF CONTENTS
[1. Introduction] [2. Development of...] [3. Vortex merging] [4. Discussion] [References] [Figures]
1. Introduction
 Like-sign vortices merge in rotating tanks (Nof and Simon 1987
; Griffiths and Hopfinger 1987
) and in the ocean (Cresswell 1982
; Tokos et al. 1994
). Merging has been numerically modeled in a wide range of settings (Melander et al. 1988
; Verron and Valcke 1994
; Carton and Bertrand 1994
; Valcke and Verron 1997
). Presumably, the characteristics of the merged vortex are set by those
of its parents and the relevant conservation laws. But what properties are
conserved in vortex merging? Gill and Griffiths (1981)
demonstrated that, if potential vorticity and mass are conserved by
two merging anticyclones, the final state contains more energy than the initial
state. This “energy paradox” is at odds with the known spontaneous nature
of vortex merging (Cushman-Roisin 1989
). Several attempts to resolve this paradox have questioned the assumptions of potential vorticity or mass conservation (Nof 1988
; Cushman-Roisin 1989
; Pavia and Cushman-Roisin 1990
).
Like-sign vortices merge in rotating tanks (Nof and Simon 1987
; Griffiths and Hopfinger 1987
) and in the ocean (Cresswell 1982
; Tokos et al. 1994
). Merging has been numerically modeled in a wide range of settings (Melander et al. 1988
; Verron and Valcke 1994
; Carton and Bertrand 1994
; Valcke and Verron 1997
). Presumably, the characteristics of the merged vortex are set by those
of its parents and the relevant conservation laws. But what properties are
conserved in vortex merging? Gill and Griffiths (1981)
demonstrated that, if potential vorticity and mass are conserved by
two merging anticyclones, the final state contains more energy than the initial
state. This “energy paradox” is at odds with the known spontaneous nature
of vortex merging (Cushman-Roisin 1989
). Several attempts to resolve this paradox have questioned the assumptions of potential vorticity or mass conservation (Nof 1988
; Cushman-Roisin 1989
; Pavia and Cushman-Roisin 1990
).
 Once
vortices come into contact, merging takes place in two stages: fusion and
axisymmetrization. During fusion, the vortices rapidly exchange fluid and
homogenize into a central, elliptical vortex. In the subsequent, relatively
slow axisymmetrization stage, the elongated vortex becomes S-shaped and sheds
part of its mass into spiral-shaped filaments while its core becomes circular.
This inviscid process is particularly dramatic in potential-vorticity-conserving
numerical models (Melander et al. 1988
; Pavia and Cushman-Roisin 1988
) and has been observed in tank experiments (Griffiths and Hopfinger 1987
). Cushman-Roisin (1989)
proposed that filamentation plays a fundamental role in the merging,
acting to relax mass conservation in the framework of the Gill and Griffiths (1981)
merging model.1 He also introduced an
additional constraint, conservation of the absolute angular momentum (the
angular momentum formulated in the inertial reference frame). He argued that
this angular momentum must be conserved in the final vortex if the merging
is complete, a condition not met by the solutions of Gill and Griffiths (1981)
(Pavia and Cushman-Roisin 1990
).
Once
vortices come into contact, merging takes place in two stages: fusion and
axisymmetrization. During fusion, the vortices rapidly exchange fluid and
homogenize into a central, elliptical vortex. In the subsequent, relatively
slow axisymmetrization stage, the elongated vortex becomes S-shaped and sheds
part of its mass into spiral-shaped filaments while its core becomes circular.
This inviscid process is particularly dramatic in potential-vorticity-conserving
numerical models (Melander et al. 1988
; Pavia and Cushman-Roisin 1988
) and has been observed in tank experiments (Griffiths and Hopfinger 1987
). Cushman-Roisin (1989)
proposed that filamentation plays a fundamental role in the merging,
acting to relax mass conservation in the framework of the Gill and Griffiths (1981)
merging model.1 He also introduced an
additional constraint, conservation of the absolute angular momentum (the
angular momentum formulated in the inertial reference frame). He argued that
this angular momentum must be conserved in the final vortex if the merging
is complete, a condition not met by the solutions of Gill and Griffiths (1981)
(Pavia and Cushman-Roisin 1990
).
 Cushman-Roisin’s (1989)
model assumes that the potential vorticity of each fluid parcel is
conserved. He concludes that a significant fraction of the initial mass must
be shed into filaments. However, when Nof and Simon (1987)
allowed anticyclonic lenses to merge in a rotating tank, the initial
vortex mass was conserved in the merged vortex (i.e., filamentation was negligible).
Furthermore, the central depth of the vortices rapidly decreased as they
fused. This depth must increase to conserve potential vorticity, suggesting
that potential vorticity is not conserved during fusion (Nof and Simon 1987
). Nof (1988)
argued that highly viscous, turbulent mixing occurs along the interface of the vortices, which can cause an O(1) alteration in the fluid parcel’s potential vorticity (Nof 1986
). This hypothesis suggests that the energy paradox can be resolved
by relaxing the a priori assumption of potential vorticity conservation.
However, Pavia and Cushman-Roisin (1990)
examined solutions to the merging model that conserve mass and energy
in the final vortex; they argued that angular momentum was not in general
conserved, rendering these solutions physically unacceptable.
Cushman-Roisin’s (1989)
model assumes that the potential vorticity of each fluid parcel is
conserved. He concludes that a significant fraction of the initial mass must
be shed into filaments. However, when Nof and Simon (1987)
allowed anticyclonic lenses to merge in a rotating tank, the initial
vortex mass was conserved in the merged vortex (i.e., filamentation was negligible).
Furthermore, the central depth of the vortices rapidly decreased as they
fused. This depth must increase to conserve potential vorticity, suggesting
that potential vorticity is not conserved during fusion (Nof and Simon 1987
). Nof (1988)
argued that highly viscous, turbulent mixing occurs along the interface of the vortices, which can cause an O(1) alteration in the fluid parcel’s potential vorticity (Nof 1986
). This hypothesis suggests that the energy paradox can be resolved
by relaxing the a priori assumption of potential vorticity conservation.
However, Pavia and Cushman-Roisin (1990)
examined solutions to the merging model that conserve mass and energy
in the final vortex; they argued that angular momentum was not in general
conserved, rendering these solutions physically unacceptable.
 In this note, we examine an analytical model of vortex merging similar to those of Gill and Griffiths (1981)
and Pavia and Cushman-Roisin (1990)
. We examine Nof’s (1988)
hypothesis for resolving the energy paradox by relaxing the constraint
of potential vorticity conservation. We formulate angular momentum conservation
in the inertial reference frame; unlike Cushman-Roisin (1989)
and Pavia and Cushman-Roisin (1990)
, we include the fluid that surrounds the merging vortices. While this
fluid is assumed to remain quiescent, it bears absolute angular momentum,
which is altered when the fluid is rearranged during merging. We demonstrate
that the absolute angular momentum of the total system, vortices and surrounding
fluid, is equal to the background angular momentum (the absolute angular
momentum in the absence of vortices), plus the sum of the vortex relative
angular momentum (the angular momentum seen in the rotating reference frame).
As a consequence, conservation of the total absolute angular momentum is
equivalent to conservation of the relative angular momentum of the vortices.
We conclude that solutions exist for the merging model that do not present
an energy or angular momentum paradox. Using a generalized model of the vortex
structure, we present two possible merging scenarios based on the choices
of conserved quantities. In the discussion, we highlight the difference between
our formulation of angular momentum conservation and that of Cushman-Roisin (1989)
and discuss physical mechanisms that can account for reduced mass or energy in the final state.
In this note, we examine an analytical model of vortex merging similar to those of Gill and Griffiths (1981)
and Pavia and Cushman-Roisin (1990)
. We examine Nof’s (1988)
hypothesis for resolving the energy paradox by relaxing the constraint
of potential vorticity conservation. We formulate angular momentum conservation
in the inertial reference frame; unlike Cushman-Roisin (1989)
and Pavia and Cushman-Roisin (1990)
, we include the fluid that surrounds the merging vortices. While this
fluid is assumed to remain quiescent, it bears absolute angular momentum,
which is altered when the fluid is rearranged during merging. We demonstrate
that the absolute angular momentum of the total system, vortices and surrounding
fluid, is equal to the background angular momentum (the absolute angular
momentum in the absence of vortices), plus the sum of the vortex relative
angular momentum (the angular momentum seen in the rotating reference frame).
As a consequence, conservation of the total absolute angular momentum is
equivalent to conservation of the relative angular momentum of the vortices.
We conclude that solutions exist for the merging model that do not present
an energy or angular momentum paradox. Using a generalized model of the vortex
structure, we present two possible merging scenarios based on the choices
of conserved quantities. In the discussion, we highlight the difference between
our formulation of angular momentum conservation and that of Cushman-Roisin (1989)
and discuss physical mechanisms that can account for reduced mass or energy in the final state.
2. Development of the model
 The model has two layers: the upper layer (density
The model has two layers: the upper layer (density 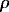 ) extends from z = 0 to z =
) extends from z = 0 to z =  H1 and the lower layer (density
H1 and the lower layer (density 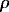 +
+ 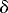
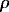 ) extends from z =
) extends from z =  H1 to z =
H1 to z =  H2 (Fig. 1
H2 (Fig. 1  ). The system is rotating at angular speed
). The system is rotating at angular speed  (Fig. 2
(Fig. 2  ) and is subject to a potential that includes gravity and centrifugal force (the familiar f-plane
approximation). Before merging, there are two identical, azimuthally symmetric
vortices in the upper layer, touching at a single point. We assume that the
fluid is reorganized into quiescent fluid surrounding a single vortex. We
assume that the final vortex has the same velocity structure as its parents;
for example, vortices in solid-body rotation merge to produce a vortex also
in solid-body rotation (though not necessarily rotating at the same rate).
Because we assume the vortices are in contact at time t = 0, we do not address the sensitivity of merging on the initial separation distance of the vortices.
) and is subject to a potential that includes gravity and centrifugal force (the familiar f-plane
approximation). Before merging, there are two identical, azimuthally symmetric
vortices in the upper layer, touching at a single point. We assume that the
fluid is reorganized into quiescent fluid surrounding a single vortex. We
assume that the final vortex has the same velocity structure as its parents;
for example, vortices in solid-body rotation merge to produce a vortex also
in solid-body rotation (though not necessarily rotating at the same rate).
Because we assume the vortices are in contact at time t = 0, we do not address the sensitivity of merging on the initial separation distance of the vortices.
a. Mass and angular momentum of an isolated vortex
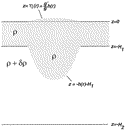
 Consider a vortex in the upper layer with radius ro, extending vertically from the surface z =
Consider a vortex in the upper layer with radius ro, extending vertically from the surface z =  (r) to z =
(r) to z =  H1
H1  h(r) (
h(r) (
Fig. 1  ). The surface deflection
). The surface deflection  is related to the azimuthal speed
is related to the azimuthal speed  by cyclogeostrophy:
by cyclogeostrophy: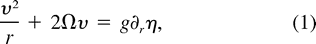
where r is the radial distance from the vortex center and g is gravity. Since there are no horizontal pressure gradients in the lower layer,
where the reduced gravity g is g
is g /g =
/g = 
 /
/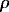 . The total mass of the vortex isM = mH + mh + m
. The total mass of the vortex isM = mH + mh + m ,
, (3)
(3)
where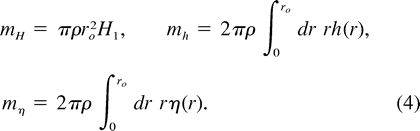
With (2), it follows that
In the rotating frame, the relative angular momentum2 of the vortex is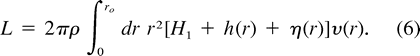
In the inertial frame, the vortex is centered at R = Ro (the position of R = 0, the axis of rotation, does not affect the solutions). Its absolute angular momentum is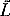 = L + MR2o
= L + MR2o + (IH + Ih + I
+ (IH + Ih + I )
)
 (7)
(7)
(the tilde indicating absolute quantities expressed in the inertial frame), where the moments of inertia are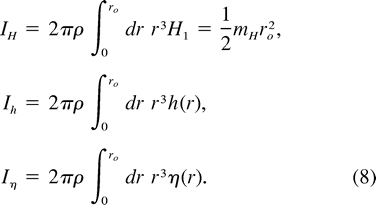
Using (2), it follows that
b. Angular momentum of vortices immersed in quiescent fluid
 In the absence of vortices, the absolute angular momentum of the quiescent background state would be
In the absence of vortices, the absolute angular momentum of the quiescent background state would be
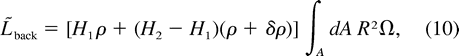
where the integral is taken over an arbitrary finite domain A.
 In the presence of N vortices (denoted by the subscript
In the presence of N vortices (denoted by the subscript  = 1, ·
= 1, · ·
· ·
· , N), the absolute angular momentum of the quiescent surrounding fluid is
, N), the absolute angular momentum of the quiescent surrounding fluid is
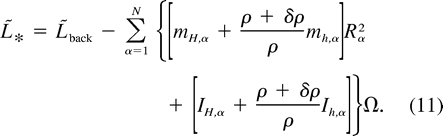
This is less than 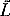 back because the vortices occupy some volume below z = 0. The absolute angular momentum of the total system (with N vortices) is obtained by adding (7) and (11):
back because the vortices occupy some volume below z = 0. The absolute angular momentum of the total system (with N vortices) is obtained by adding (7) and (11):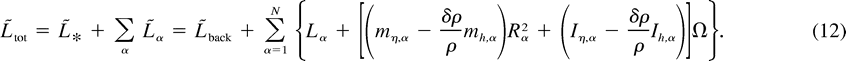
Vortices extend to height  above z = 0; revolution and rotation of this mass at speed
above z = 0; revolution and rotation of this mass at speed  adds angular momentum to the background state. Similarly, vortices extend a distance h
adds angular momentum to the background state. Similarly, vortices extend a distance h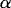 into the lower layer; because this fluid is lower in density, it subtracts angular momentum from the background state. Using (5) and (9), (12) simplifies to
into the lower layer; because this fluid is lower in density, it subtracts angular momentum from the background state. Using (5) and (9), (12) simplifies to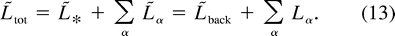
Angular
momentum added by surface bulges is equal to angular momentum subtracted
by layer interface bulges, and they cancel. The absolute angular momentum
of the entire system differs from the angular momentum of the background
state only by the sum of the relative angular momentum of the vortices.
c. Energy of vortices
 The
fluid in the rotating reference frame is subject to a potential that includes
the centrifugal force. In the inertial frame, the potential consists of only
gravity, complicating the formulation of energy conservation in that frame.
Thus, following
The
fluid in the rotating reference frame is subject to a potential that includes
the centrifugal force. In the inertial frame, the potential consists of only
gravity, complicating the formulation of energy conservation in that frame.
Thus, following
Gill and Griffiths (1981)
and Cushman-Roisin (1989)
, we examine the energy of the vortices in the algebraically simpler
rotating reference frame, that is, using the familiar definitions of the
kinetic and potential energy, the sum of which is invariant for a closed
system (Gill 1982
, p. 220). The kinetic energy of a vortex is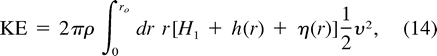
and the potential energy is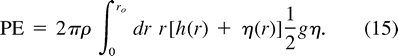
The net energy E = KE + PE may be related to the relative angular momentum as follows. The relative angular momentum L is given by (6). From cyclogeostrophy (1),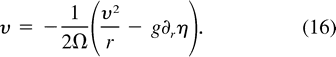
Substitution yields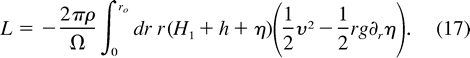
The term containing 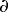 r
r may be integrated by parts, yielding
may be integrated by parts, yielding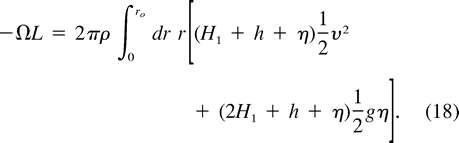
Using (4), (14), and (15), this becomesE = 
 L
L  gH1m
gH1m .
. (19)
(19)
The total energy of N vortices is then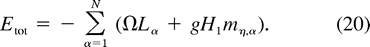
If H1 = 0, that is, the vortices are lens-shaped, their energy is proportional to their relative angular momentum.
3. Vortex merging
 When two identical vortices (denoted by subscripts a and b) merge to produce a single vortex (c) without entraining surrounding fluid, mass conservation requires
When two identical vortices (denoted by subscripts a and b) merge to produce a single vortex (c) without entraining surrounding fluid, mass conservation requires
Mc = Ma + Mb, (21)
(21)
where the masses are given by (3). By definition, the background angular momentum
By definition, the background angular momentum  back remains unchanged. Thus, from (13), conservation of angular momentum requires
back remains unchanged. Thus, from (13), conservation of angular momentum requires
Lc = La + Lb. (22)
(22)
Conservation of the absolute angular momentum reduces to conservation of the relative angular momentum of the vortices.3 From (20), energy conservation Ec = Ea + Eb requires
From (20), energy conservation Ec = Ea + Eb requires
 Lc + gH1m
Lc + gH1m ,c =
,c =  La + gH1m
La + gH1m ,a +
,a +  Lb + gH1m
Lb + gH1m ,b.
,b. (23)
(23)
Mass, angular momentum, and energy can be simultaneously conserved when eitherm ,c = m
,c = m ,a + m
,a + m ,b
,b (24)
(24)
or H1 = 0. We now examine the merging properties of particular vortex structures.
We now examine the merging properties of particular vortex structures.
a. Solid-body vortices
 A solid-body vortex has the velocity structure
A solid-body vortex has the velocity structure  (r) =
(r) =  r, where
r, where  is constant. By imposing
is constant. By imposing  = 0 at r = ro, cyclogeostrophy (1) may be integrated to yield
= 0 at r = ro, cyclogeostrophy (1) may be integrated to yield
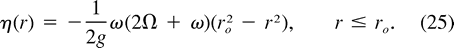
The relative angular momentum isL = (IH + Ih + I )
) .
. (26)
(26)
 Consider two identical solid-body vortices (a and b) merging to produce vortex c, assumed to be also in solid-body rotation. Given
Consider two identical solid-body vortices (a and b) merging to produce vortex c, assumed to be also in solid-body rotation. Given  a,
a,  b, ra, and rb, two independent conservation laws determine
b, ra, and rb, two independent conservation laws determine  c and rc. This leads to the dilemma faced by Pavia and Cushman-Roisin (1990)
: which of the three constraints (mass, angular momentum, and energy
conservation) should apply? Following Pavia and Cushman-Roisin, we consider
two separate merging scenarios; in each we conserve two of these properties
and examine what happens to the third. Physical interpretations of the results
will be discussed in the final section. We restrict the development to the
particular case of identical merging vortices (
c and rc. This leads to the dilemma faced by Pavia and Cushman-Roisin (1990)
: which of the three constraints (mass, angular momentum, and energy
conservation) should apply? Following Pavia and Cushman-Roisin, we consider
two separate merging scenarios; in each we conserve two of these properties
and examine what happens to the third. Physical interpretations of the results
will be discussed in the final section. We restrict the development to the
particular case of identical merging vortices ( a =
a =  b, ra = rb), and reject values of (
b, ra = rb), and reject values of ( a, ra) that yield a nonpositive central thickness H1 + h(r) +
a, ra) that yield a nonpositive central thickness H1 + h(r) +  (r).
(r).
 1) CONSERVING MASS AND ANGULAR MOMENTUM
1) CONSERVING MASS AND ANGULAR MOMENTUM
Figure 3  shows the values of
shows the values of  c and rc, which conserve mass and angular momentum. Several curves are shown, each corresponding to a fixed ratio of ra to the internal Rossby radius Rd:
c and rc, which conserve mass and angular momentum. Several curves are shown, each corresponding to a fixed ratio of ra to the internal Rossby radius Rd:
In the limit H1  0 or ra/Rd
0 or ra/Rd 
 , the vortices become anticyclonic lenses; in particular, zero potential vorticity lenses (
, the vortices become anticyclonic lenses; in particular, zero potential vorticity lenses ( 1 =
1 = 
 ) merge such that
) merge such that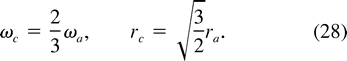
In the limit H1 
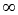 or ra/Rd
or ra/Rd  0, the vortices become 2D cylinders that merge such that
0, the vortices become 2D cylinders that merge such that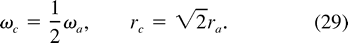
The bottom panel of Fig. 3  shows the ratio of final energy Ec to initial energy 2Ea. For lens-shaped anticyclonic vortices, energy is conserved. However, for finite ra/Rd, energy must be lost in the merging; the loss reaches 50% at the limit of cylindrical vortices.
shows the ratio of final energy Ec to initial energy 2Ea. For lens-shaped anticyclonic vortices, energy is conserved. However, for finite ra/Rd, energy must be lost in the merging; the loss reaches 50% at the limit of cylindrical vortices.
 2) CONSERVING ANGULAR MOMENTUM AND ENERGY
2) CONSERVING ANGULAR MOMENTUM AND ENERGY
Figure 4  shows the values of
shows the values of  c and rc, which conserve angular momentum and energy. Compared to the mass-conserving scenario (Fig. 3
c and rc, which conserve angular momentum and energy. Compared to the mass-conserving scenario (Fig. 3  ), the change in period (
), the change in period ( a/
a/ c) is smaller for a given ra/Rd and decreases with decreasing ra/Rd; the final radius is also smaller. For finite ra/Rd, the final vortex has less mass than the initial two vortices. At the limit of cylindrical vortices (ra/Rd
c) is smaller for a given ra/Rd and decreases with decreasing ra/Rd; the final radius is also smaller. For finite ra/Rd, the final vortex has less mass than the initial two vortices. At the limit of cylindrical vortices (ra/Rd  0), the mass loss is Mc/2Ma = 1/
0), the mass loss is Mc/2Ma = 1/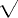 (2). For lens-shaped anticyclonic vortices (ra/Rd =
(2). For lens-shaped anticyclonic vortices (ra/Rd =  ), mass is conserved.
), mass is conserved.
b. Vortices with finite-shear edges
 In
the solid-body model, vortices have an infinite-shear edge separating vortex
fluid from surrounding upper-layer fluid of identical density. However, momentum
diffusion would rapidly smear the edge vorticity into a shell surrounding
the solid-body core. Within this shell,
In
the solid-body model, vortices have an infinite-shear edge separating vortex
fluid from surrounding upper-layer fluid of identical density. However, momentum
diffusion would rapidly smear the edge vorticity into a shell surrounding
the solid-body core. Within this shell,  (r) decreases with increasing r.
If the shell’s width is allowed to adjust during merging, its inclusion in
the model adds a degree of freedom to the solutions. Consider vortices with
the velocity structure:
(r) decreases with increasing r.
If the shell’s width is allowed to adjust during merging, its inclusion in
the model adds a degree of freedom to the solutions. Consider vortices with
the velocity structure:
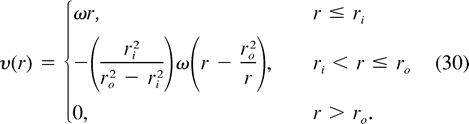
The azimuthal speed  is continuous at r = ri, ro (Fig. 5
is continuous at r = ri, ro (Fig. 5  ). The solid-body core extends to r = ri, and is surrounded by a constant vorticity shell extending to r = ro. Outside this shell, there is no circulation induced by the vortex [i.e., this is an “exactly shielded” vortex as defined by Carton and Bertrand (1994)
]. The vortices are completely included over an arbitrary finite domain. The ratio of shell vorticity
). The solid-body core extends to r = ri, and is surrounded by a constant vorticity shell extending to r = ro. Outside this shell, there is no circulation induced by the vortex [i.e., this is an “exactly shielded” vortex as defined by Carton and Bertrand (1994)
]. The vortices are completely included over an arbitrary finite domain. The ratio of shell vorticity  o to core vorticity
o to core vorticity  i is
i is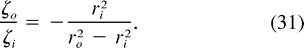
In the limit ro  ri, the outer shell is nearly irrotational and the vortex becomes Rankine-like. If ro <
ri, the outer shell is nearly irrotational and the vortex becomes Rankine-like. If ro < 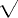 (2)ri, the magnitude of the shell vorticity is larger than that of the core vorticity.
(2)ri, the magnitude of the shell vorticity is larger than that of the core vorticity.
 Vortices
of this structure may be centrifugally unstable. If a fluid parcel orbiting
a cyclogeostrophic vortex is infinitesmally perturbed, it experiences a restoring
force proportional to
Vortices
of this structure may be centrifugally unstable. If a fluid parcel orbiting
a cyclogeostrophic vortex is infinitesmally perturbed, it experiences a restoring
force proportional to
F = 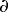 r(
r( r +
r +  r2)2
r2)2 (32)
(32)
(Kloosterziel and van Heijst 1991
). If F < 0 anywhere in the vortex, perturbations will grow
exponentially. Applying this stability criterion to the inner edge of the
shell shows that anticyclones are unstable if 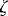 i <
i < 
 , while cyclones are unstable if the anticyclonic shell vorticity
, while cyclones are unstable if the anticyclonic shell vorticity  o is less than
o is less than 
 .
Thus, rapidly spinning anticyclones and narrow-shelled cyclones are unstable.
In this paper, we do not explore solutions in the (
.
Thus, rapidly spinning anticyclones and narrow-shelled cyclones are unstable.
In this paper, we do not explore solutions in the ( , ri, ro)
parameter space describing unstable vortices. We also discard choices of
these parameters that yield nonpositive central depths for the cyclonic vortices.
, ri, ro)
parameter space describing unstable vortices. We also discard choices of
these parameters that yield nonpositive central depths for the cyclonic vortices.
 There is no guarantee that the set of nonlinear conservation laws can be simultaneously satisfied by a unique combination of
There is no guarantee that the set of nonlinear conservation laws can be simultaneously satisfied by a unique combination of  c, ri,c, and ro,c.
Paralleling the solid-body case, we examine two merging scenarios: one in
which mass is conserved a priori and the other in which energy is conserved.
In both scenarios, we assume that the mass Mi of the solid-body core is conserved:
c, ri,c, and ro,c.
Paralleling the solid-body case, we examine two merging scenarios: one in
which mass is conserved a priori and the other in which energy is conserved.
In both scenarios, we assume that the mass Mi of the solid-body core is conserved:
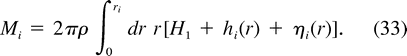
 This
constraint demands that fluid parcels retain the sign of their vorticity;
that is, the core of the merged vortex is the fused cores of the initial
vortices, and mass changes in the energy-conserving scenario are associated
solely with shell fluid.4
This
constraint demands that fluid parcels retain the sign of their vorticity;
that is, the core of the merged vortex is the fused cores of the initial
vortices, and mass changes in the energy-conserving scenario are associated
solely with shell fluid.4
 1) CONSERVING TOTAL MASS AND ANGULAR MOMENTUM
1) CONSERVING TOTAL MASS AND ANGULAR MOMENTUM
Figure 6  shows the characteristics of the merged vortex (
shows the characteristics of the merged vortex ( c, ri,c and ro,c) as functions of
c, ri,c and ro,c) as functions of  a/
a/ for ro,a/ri,a = 10. Compared to the solid-body counterpart to this scenario (Fig. 3
for ro,a/ri,a = 10. Compared to the solid-body counterpart to this scenario (Fig. 3  ), the period jump
), the period jump  a/
a/ c is closer to 2 and the radius jump ri,c/ri,a is closer to
c is closer to 2 and the radius jump ri,c/ri,a is closer to  (2), that is, closer to those of the limiting case of infinite cylinders.
(2), that is, closer to those of the limiting case of infinite cylinders.
 The energy loss is nearly independent of
The energy loss is nearly independent of  a/
a/ . Energy is lost for small ri,a/Rd, but less so than in the solid-body counterpart (Fig. 3
. Energy is lost for small ri,a/Rd, but less so than in the solid-body counterpart (Fig. 3  ). For ri,a/Rd
). For ri,a/Rd  8, energy is conserved within 0.1% for all values of
8, energy is conserved within 0.1% for all values of  a/
a/ .
.
 Figure 7
Figure 7  shows how the characteristics of the merged vortex vary as a function of shell width ro,a/ri,a, for the limiting case of a zero potential vorticity anticyclonic core (
shows how the characteristics of the merged vortex vary as a function of shell width ro,a/ri,a, for the limiting case of a zero potential vorticity anticyclonic core ( a/
a/ =
=  1). For nearly irrotational shells (ro,a
1). For nearly irrotational shells (ro,a  ri,a), the merged vortex has a core period nearly double that of the original vortices (
ri,a), the merged vortex has a core period nearly double that of the original vortices ( a/
a/ c
c 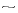 2) and inner and outer radii larger by
2) and inner and outer radii larger by 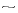
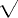 (2). The dependence of the solutions on ri,a/Rd increases as ro,a
(2). The dependence of the solutions on ri,a/Rd increases as ro,a  ri,a (the solid-body limit), and energy is lost (particularly for small ri,a/Rd).
ri,a (the solid-body limit), and energy is lost (particularly for small ri,a/Rd).
 2) CONSERVING ANGULAR MOMENTUM AND ENERGY
2) CONSERVING ANGULAR MOMENTUM AND ENERGY
Figure 8  shows the characteristics of the merged vortex for ro,a/ri,a = 10. Compared to the solid-body counterpart of this scenario (Fig. 4
shows the characteristics of the merged vortex for ro,a/ri,a = 10. Compared to the solid-body counterpart of this scenario (Fig. 4  ),
),  a/
a/ c is again closer to 2 and ro,c/ro,a is closer to
c is again closer to 2 and ro,c/ro,a is closer to 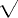 (2), that is, closer to those of infinite cylinders.
(2), that is, closer to those of infinite cylinders.
 Mass is conserved in the limit ri,a
Mass is conserved in the limit ri,a  Rd. Smaller vortices lose mass when they merge, nearly independently of
Rd. Smaller vortices lose mass when they merge, nearly independently of  a/
a/ . For ri,a = Rd, 7%–8% of the mass is lost in the merging.
. For ri,a = Rd, 7%–8% of the mass is lost in the merging.
 Figure 9
Figure 9  shows the characteristics of the merged vortex as a function of ro,a/ri,a, for
shows the characteristics of the merged vortex as a function of ro,a/ri,a, for  a/
a/ =
=  1. For vortices with nearly irrotational shells, mass is conserved. The mass loss exceeds 10% for shell radius smaller than ro,a/Rd
1. For vortices with nearly irrotational shells, mass is conserved. The mass loss exceeds 10% for shell radius smaller than ro,a/Rd 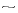 10.
10.
4. Discussion
 Although we assume that the surrounding fluid remains quiescent, when the total depth H2
is finite, fluid columns underlying the vortices may be compressed or stretched
in the merging. A column of quiescent fluid beneath a vortex bears potential
vorticity 2
Although we assume that the surrounding fluid remains quiescent, when the total depth H2
is finite, fluid columns underlying the vortices may be compressed or stretched
in the merging. A column of quiescent fluid beneath a vortex bears potential
vorticity 2 /(H2
/(H2  H1
H1  h), where h is the downward displacement of the interface. If during merging h increases by
h), where h is the downward displacement of the interface. If during merging h increases by 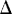 h, the underlying column must gain anticyclonic vorticity
h, the underlying column must gain anticyclonic vorticity 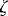 ,
,
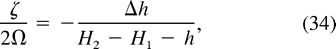
in
order to conserve its angular momentum. Thus, the assumption of a “quiescent
surrounding fluid,” which allowed us to simplify angular momentum conservation,
is valid in the limit H2 
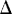 h and exact in the 1˝-layer limit H2
h and exact in the 1˝-layer limit H2 
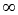 .
This limit is appropriate for midlatitude open ocean baroclinic eddies, but
does not apply to lens-shaped vortices whose height are an appreciable fraction
of the total water depth (Nof and Simon 1987
). In this case, cyclonic motion induced in the second layer contributes significantly to the total energy of the system (Dewar and Killworth 1990
).
.
This limit is appropriate for midlatitude open ocean baroclinic eddies, but
does not apply to lens-shaped vortices whose height are an appreciable fraction
of the total water depth (Nof and Simon 1987
). In this case, cyclonic motion induced in the second layer contributes significantly to the total energy of the system (Dewar and Killworth 1990
). In their examination of lens-shaped vortex merging, Pavia and Cushman-Roisin (1990)
conserved the mass and energy of the initial vortices, and showed that
the absolute angular momentum of the vortices was not conserved. However,
there is no “angular momentum paradox” inherent in their result, due to the
role of the surrounding fluid in the total angular momentum budget. A simple
thought experiment can serve to highlight this role: consider a pair of cylinders
(density
In their examination of lens-shaped vortex merging, Pavia and Cushman-Roisin (1990)
conserved the mass and energy of the initial vortices, and showed that
the absolute angular momentum of the vortices was not conserved. However,
there is no “angular momentum paradox” inherent in their result, due to the
role of the surrounding fluid in the total angular momentum budget. A simple
thought experiment can serve to highlight this role: consider a pair of cylinders
(density 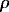 , mass ma, radius ra in solid-body rotation at relative rate
, mass ma, radius ra in solid-body rotation at relative rate  a) touching at the center of a tank that rotates at
a) touching at the center of a tank that rotates at  . The cylinders are surrounded by fluid of density
. The cylinders are surrounded by fluid of density 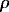
 . Later, they have merged to produce a single cylinder of the same density with mass mc = 2ma, radius rc, and rotation rate
. Later, they have merged to produce a single cylinder of the same density with mass mc = 2ma, radius rc, and rotation rate  c. It is centered on the contact point of the parent vortices. Conservation of mass requires rc =
c. It is centered on the contact point of the parent vortices. Conservation of mass requires rc = 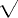 (2)ra, and angular momentum conservation for the entire system requires
(2)ra, and angular momentum conservation for the entire system requires
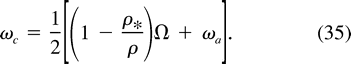
In the absence of surrounding fluid, 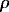
 = 0, and (35) becomes
= 0, and (35) becomes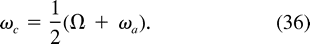
 This expression is analogous to the formulation of angular momentum conservation of Cushman-Roisin (1989)
and Pavia and Cushman-Roisin (1990)
. With
This expression is analogous to the formulation of angular momentum conservation of Cushman-Roisin (1989)
and Pavia and Cushman-Roisin (1990)
. With 
 = 0, we are essentially considering coalescing fixed-height disks on a rotating
table. To an observer in the rotating frame, the rotation rate of the resulting
disk is more positive (for positive
= 0, we are essentially considering coalescing fixed-height disks on a rotating
table. To an observer in the rotating frame, the rotation rate of the resulting
disk is more positive (for positive  )
than it would be in the absence of rotation, due to Coriolis deflection applying
a net torque on the coalescing particles (cf. Feynman et al. 1987
, p. 19-8). However, if
)
than it would be in the absence of rotation, due to Coriolis deflection applying
a net torque on the coalescing particles (cf. Feynman et al. 1987
, p. 19-8). However, if 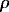
 =
= 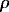 , (35) simplifies to
, (35) simplifies to

that
is, the period doubles and relative angular momentum is conserved. As the
cylinders coalesce, they lose the absolute angular momentum associated with
revolution about their contact point, but this is balanced by the absolute
angular momentum gained by the displaced surrounding fluid. In the rotating
frame, Coriolis deflection of the coalescing parcels is balanced by a pressure
gradient in the surrounding fluid (Rossby 1936
, 1948
). Our model demonstrates that solid-body vortices can conserve mass, angular momentum, and energy in the lens-shaped limit H1 = 0. For nonzero H1 either energy or mass conservation must be relaxed, leading to the two merging scenarios discussed in this paper.5
In the first scenario, if mass is conserved, the final vortex has less total
energy than its parents. These solutions are thus “energetically allowable”
(Dewar and Killworth 1990
) in the sense that an external energy source is not required, analogous
to the classical Rossby adjustment problem that has a steady-state solution
with one-third of the initial energy (cf. Gill 1982
, pp. 191–203), the remaining energy having been removed via Poincaré
wave radiation. Turbulent mixing during merging can also lower the energy
state of the merged vortex (Nof 1986
).
Our model demonstrates that solid-body vortices can conserve mass, angular momentum, and energy in the lens-shaped limit H1 = 0. For nonzero H1 either energy or mass conservation must be relaxed, leading to the two merging scenarios discussed in this paper.5
In the first scenario, if mass is conserved, the final vortex has less total
energy than its parents. These solutions are thus “energetically allowable”
(Dewar and Killworth 1990
) in the sense that an external energy source is not required, analogous
to the classical Rossby adjustment problem that has a steady-state solution
with one-third of the initial energy (cf. Gill 1982
, pp. 191–203), the remaining energy having been removed via Poincaré
wave radiation. Turbulent mixing during merging can also lower the energy
state of the merged vortex (Nof 1986
).
 In the second scenario, if energy is conserved, the final vortex has less mass than its parents. Cushman-Roisin (1989)
proposed that merging vortices eject fluid in narrow filaments as they become axisymmetric (Griffiths and Hopfinger 1987
; Melander et al. 1988
). Because these filaments bear negligible energy and relative angular
momentum but a significant fraction of the mass, they are modeled implicitly
by relaxing mass conservation, as was done in the second scenario (Pavia and Cushman-Roisin 1990
).
In the second scenario, if energy is conserved, the final vortex has less mass than its parents. Cushman-Roisin (1989)
proposed that merging vortices eject fluid in narrow filaments as they become axisymmetric (Griffiths and Hopfinger 1987
; Melander et al. 1988
). Because these filaments bear negligible energy and relative angular
momentum but a significant fraction of the mass, they are modeled implicitly
by relaxing mass conservation, as was done in the second scenario (Pavia and Cushman-Roisin 1990
).
 In
summary, vortices can conserve mass, angular momentum, and energy when they
merge in two physically important limits of vortex structure: lens-shaped
anticyclones and Rankine-like eddies. All three properties cannot be simultaneously
conserved over the full range of parameters considered here; in general,
mass or energy must be lost, presumably due to Poincaré wave radiation, turbulent
dissipation, or filamentation. Future laboratory experiments and field observations
could determine which scenario best describes the merging of oceanic vortices.
In
summary, vortices can conserve mass, angular momentum, and energy when they
merge in two physically important limits of vortex structure: lens-shaped
anticyclones and Rankine-like eddies. All three properties cannot be simultaneously
conserved over the full range of parameters considered here; in general,
mass or energy must be lost, presumably due to Poincaré wave radiation, turbulent
dissipation, or filamentation. Future laboratory experiments and field observations
could determine which scenario best describes the merging of oceanic vortices.
 Acknowledgments.
The authors would like to thank B. Cushman-Roisin, J. Verron, E. Hopfinger,
Gert Jan van Heijst, B. Le Cann, J. Paillet, Y. Morel, and X. Carton for
valuable conversations on the subjects of vortex dynamics and merging. Support
for P. Flament and R. Lumpkin was provided by Office of Naval Research Contract
N000149710147. R. C. Kloosterziel and P. Flament received support from National
Science Foundation Grant OCE 97-30843. R. Lumpkin would like to thank IFREMER
for hosting during a French Minister of Foreign Affairs postdoctoral fellowship.
Acknowledgments.
The authors would like to thank B. Cushman-Roisin, J. Verron, E. Hopfinger,
Gert Jan van Heijst, B. Le Cann, J. Paillet, Y. Morel, and X. Carton for
valuable conversations on the subjects of vortex dynamics and merging. Support
for P. Flament and R. Lumpkin was provided by Office of Naval Research Contract
N000149710147. R. C. Kloosterziel and P. Flament received support from National
Science Foundation Grant OCE 97-30843. R. Lumpkin would like to thank IFREMER
for hosting during a French Minister of Foreign Affairs postdoctoral fellowship.
REFERENCES
Carton, X., and C. Bertrand, 1994: The influence of environmental parameters on two-dimensional vortex merger. Modelling of Oceanic Vortices, G. J. Heijst, Ed., North-Holland, 125–134.
Cresswell, G. R., 1982: The coalescence of two East Australian current warm-core eddies. Science, 215, 161–164.
Cushman-Roisin, B., 1989: On the role of filamentation in the merging of anticyclonic lenses. J. Phys. Oceanogr., 19, 253–258.
Dewar, W. K., and P. D. Killworth, 1990: On the cylinder collapse problem, mixing, and the merger of isolated eddies. J. Phys. Oceanogr., 20, 1563–1575.
Feynman, R. P., R. B. Leighton, and M. L. Sands, 1987: The Feynman Lectures on Physics. Addison-Wesley.
Gill, A. E., 1982: Atmosphere–Ocean Dynamics. International Geophysics Series, Vol. 30, Academic Press, 662 pp.
——, and R. W. Griffiths, 1981: Why should two anticyclonic eddies merge? Ocean Modelling (unpublished manuscripts), 41, 10–16.
Griffiths, R. W., and E. J. Hopfinger, 1987: Coalescing of geostrophic vortices. J. Fluid Mech., 178, 73–97.
Kloosterziel, R. C., and G. J. Heijst, 1991: An experimental study of unstable barotropic vortices in a rotating fluid. J. Fluid Mech., 223, 1–24.
Melander, M. V., N. J. Zabusky, and J. C. McWilliams, 1988: Symmetric vortex merger in two dimensions: Causes and conditions. J. Fluid Mech., 195, 303–340.
Nof, D., 1986: Geostrophic shock waves. J. Phys. Oceanogr., 16, 886–901.
——, 1988: The fusion of isolated nonlinear eddies. J. Phys. Oceanogr., 18, 887–905.
——, and L. M. Simon, 1987: Laboratory experiments on the merging of nonlinear anticyclonic eddies. J. Phys. Oceanogr., 17, 343–357.
Pavia, E. G., and B. Cushman-Roisin, 1988: Modeling of oceanic fronts using a particle method. J. Geophys. Res., 93, 3554–3562.
——, and ——, 1990: Merging of frontal eddies. J. Phys. Oceanogr., 20, 1886–1906.
Rossby, C.-G., 1936: Dynamics of steady ocean currents in the light of experimental fluid mechanics. Papers in Phys. Oceanogr. Meteor., V, 1–43.
——, 1948: On displacements and intensity changes of atmospheric vortices. J. Fluid Mech., 7, 175–187.
Tokos, K. L. S., H.-H. Hinrichsen, and W. Zenk, 1994: Merging and migration of two meddies. J. Phys. Oceanogr., 24, 2129–2141.
Valcke, S., and J. Verron, 1997: Interactions of baroclinic isolated vortices: The dominant effect of shielding. J. Phys. Oceanogr., 27, 524–541.
Verron, J., and S. Valcke, 1994: Scale-dependent merging of baroclinic vortices. J. Fluid Mech., 264, 81–106.
Figures
Click on thumbnail for full-sized image.
 Fig.
1. Side view of a vortex and surrounding quiescent fluid in the 2-layer model.
For a vortex in solid-body rotation, the surface and interface displacements
are parabolic, as sketched here.
Fig.
1. Side view of a vortex and surrounding quiescent fluid in the 2-layer model.
For a vortex in solid-body rotation, the surface and interface displacements
are parabolic, as sketched here.
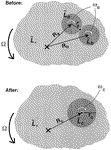
Click on thumbnail for full-sized image.
 Fig. 2. Top view of the merging model. The center of rotation of the system is at the
Fig. 2. Top view of the merging model. The center of rotation of the system is at the  .
.

Click on thumbnail for full-sized image.
 Fig. 3. Top: ratio of final rotational frequency
Fig. 3. Top: ratio of final rotational frequency  c to initial frequency
c to initial frequency  a as a function of
a as a function of  a/
a/ ,
for solid-body vortices, which conserve mass and angular momentum when they
merge. The label for each curve indicates the value of ra/Rd. The heavy line gives the solution for a lens-shaped vortex (Rd = H1 = 0). Some curves end before reaching
,
for solid-body vortices, which conserve mass and angular momentum when they
merge. The label for each curve indicates the value of ra/Rd. The heavy line gives the solution for a lens-shaped vortex (Rd = H1 = 0). Some curves end before reaching  a =
a =  ; at greater values of
; at greater values of  a, the vortex has negative thickness H1 + h +
a, the vortex has negative thickness H1 + h +  at its center and is thus not geometrically valid. Middle: ratio of final radius rc to initial radius ra as a function of
at its center and is thus not geometrically valid. Middle: ratio of final radius rc to initial radius ra as a function of  a/
a/ . Bottom: ratio of final energy Ec to initial energy 2Ea. Except in the lens-shaped case, the merged vortex has less energy.
. Bottom: ratio of final energy Ec to initial energy 2Ea. Except in the lens-shaped case, the merged vortex has less energy.

Click on thumbnail for full-sized image.
 Fig. 4. Top: ratio of final rotational frequency
Fig. 4. Top: ratio of final rotational frequency  c to initial frequency
c to initial frequency  c as a function of
c as a function of  a/
a/ ,
for solid-body vortices, which conserve angular momentum and energy when
they merge. The label for each curve indicates the value of ra/Rd. The heavy line gives the solution for a lens-shaped vortex (Rd = H1 = 0). Some curves end before reaching
,
for solid-body vortices, which conserve angular momentum and energy when
they merge. The label for each curve indicates the value of ra/Rd. The heavy line gives the solution for a lens-shaped vortex (Rd = H1 = 0). Some curves end before reaching  a =
a =  ; at greater values of
; at greater values of  a, the vortex has negative thickness H1 + h +
a, the vortex has negative thickness H1 + h +  at its center and is thus not geometrically valid. Middle: ratio of final radius rc to initial radius ra as a function of
at its center and is thus not geometrically valid. Middle: ratio of final radius rc to initial radius ra as a function of  a/
a/ . Bottom: ratio of final mass Mc to initial mass 2Ma. Except in the lens-shaped case, the merged vortex has less mass.
. Bottom: ratio of final mass Mc to initial mass 2Ma. Except in the lens-shaped case, the merged vortex has less mass.
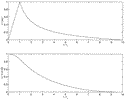
Click on thumbnail for full-sized image.
 Fig. 5. Top: azimuthal velocity
Fig. 5. Top: azimuthal velocity  (r) vs radial distance for a vortex with a constant vorticity shell surrounding a solid body core. For this vortex,
(r) vs radial distance for a vortex with a constant vorticity shell surrounding a solid body core. For this vortex,  =
= 
 . Bottom: sea surface displacement
. Bottom: sea surface displacement  vs radial distance, calculated by integrating the cyclogeostrophic relation (1).
vs radial distance, calculated by integrating the cyclogeostrophic relation (1).

Click on thumbnail for full-sized image.
 Fig. 6. Top: ratio of final rotational frequency
Fig. 6. Top: ratio of final rotational frequency  c to initial frequency
c to initial frequency  a as a function of
a as a function of  a/
a/ , for finite-shear vortices, which conserve total mass and angular momentum when they merge (ro,a = 10ri,a). The label for each curve indicates the value of ri,a/Rd. Some curves end before reaching
, for finite-shear vortices, which conserve total mass and angular momentum when they merge (ro,a = 10ri,a). The label for each curve indicates the value of ri,a/Rd. Some curves end before reaching  a =
a =  ; at greater values of
; at greater values of  a, the vortex would have negative thickness H1 + h +
a, the vortex would have negative thickness H1 + h +  at its center and is thus not geometrically valid. Middle, upper: ratio of final core radius ri,c to initial core radius ri,a. Middle, lower: ratio of final shell radius ro,c to initial shell radius ro,a. Bottom: ratio of final energy Ec to initial energy 2Ea.
at its center and is thus not geometrically valid. Middle, upper: ratio of final core radius ri,c to initial core radius ri,a. Middle, lower: ratio of final shell radius ro,c to initial shell radius ro,a. Bottom: ratio of final energy Ec to initial energy 2Ea.

Click on thumbnail for full-sized image.
 Fig. 7. Top: ratio of final rotational frequency
Fig. 7. Top: ratio of final rotational frequency  c to initial frequency
c to initial frequency  a as a function of ro,a/ri,a, for finite-shear anticyclonic vortices, which conserve total mass and angular momentum when they merge, at the limit
a as a function of ro,a/ri,a, for finite-shear anticyclonic vortices, which conserve total mass and angular momentum when they merge, at the limit  a/
a/ =
=  1. The label for each curve indicates the value of ri,a/Rd. Middle, upper: ratio of final core radius ri,c to initial core radius ri,a. Middle, lower: ratio of final shell radius ro,c to initial shell radius ro,a. Bottom: ratio of final energy Ec to initial energy 2Ea.
1. The label for each curve indicates the value of ri,a/Rd. Middle, upper: ratio of final core radius ri,c to initial core radius ri,a. Middle, lower: ratio of final shell radius ro,c to initial shell radius ro,a. Bottom: ratio of final energy Ec to initial energy 2Ea.

Click on thumbnail for full-sized image.
 Fig. 8. Top: ratio of final rotational frequency
Fig. 8. Top: ratio of final rotational frequency  c to initial frequency
c to initial frequency  a as a function of
a as a function of  a/
a/ , for finite-shear vortices, which conserve angular momentum and energy when they merge (ro,a = 10ri,a). The label for each curve indicates the value of ri,a/Rd. Some curves end before reaching
, for finite-shear vortices, which conserve angular momentum and energy when they merge (ro,a = 10ri,a). The label for each curve indicates the value of ri,a/Rd. Some curves end before reaching  a =
a =  ; at greater values of
; at greater values of  a, the vortex would have negative thickness H1 + h +
a, the vortex would have negative thickness H1 + h +  at its center and is thus not geometrically valid. Middle, upper: ratio of final core radius ri,c to initial core radius ri,a. Middle, lower: ratio of final shell radius ro,c to initial shell radius ro,a. Bottom: ratio of final mass Mc to initial mass 2Ma.
at its center and is thus not geometrically valid. Middle, upper: ratio of final core radius ri,c to initial core radius ri,a. Middle, lower: ratio of final shell radius ro,c to initial shell radius ro,a. Bottom: ratio of final mass Mc to initial mass 2Ma.

Click on thumbnail for full-sized image.
 Fig. 9. Top: ratio of final rotational frequency
Fig. 9. Top: ratio of final rotational frequency  c to initial frequency
c to initial frequency  a as a function of ro,a/ri,a, for finite-shear vortices, which conserve angular momentum and energy when they merge (
a as a function of ro,a/ri,a, for finite-shear vortices, which conserve angular momentum and energy when they merge ( a/
a/ =
=  1). The label for each curve indicates the value of ri,a/Rd. Middle, upper: ratio of final core radius ri,c to initial core radius ri,a. Middle, lower: ratio of final shell radius ro,c to initial shell radius ro,a. Bottom: ratio of final mass Mc to initial mass 2Ma.
1). The label for each curve indicates the value of ri,a/Rd. Middle, upper: ratio of final core radius ri,c to initial core radius ri,a. Middle, lower: ratio of final shell radius ro,c to initial shell radius ro,a. Bottom: ratio of final mass Mc to initial mass 2Ma.
 1
1 Cushman-Roisin
explicitly included an idealized model for the filaments, and concluded that
when zero potential vorticity lenses merge, 23% of their mass goes into the
filaments while 96% of their energy is retained in the merged vortex.
Cushman-Roisin
explicitly included an idealized model for the filaments, and concluded that
when zero potential vorticity lenses merge, 23% of their mass goes into the
filaments while 96% of their energy is retained in the merged vortex.
 2
2 Specifically, the vertical component of the angular momentum vector.
Specifically, the vertical component of the angular momentum vector.
 3
3 The
equivalency of these invariants can also be derived directly from the momentum
and continuity equations for a rotating, multilayer fluid (B. Cushman-Roisin,
1999, personal communication).
The
equivalency of these invariants can also be derived directly from the momentum
and continuity equations for a rotating, multilayer fluid (B. Cushman-Roisin,
1999, personal communication).
 4
4 When
2D vortices of the exactly shielded structure are brought into contact, their
cores merge while shell fluid is lost. However, if they have shell vorticity
greater than that given by (31)
(and consequently induce circulation around the edge of any arbitrarily large,
finite domain), their interaction in the presence of instability may cause
the shell fluid to merge while core fluid is rejected (Carton and Bertrand 1994
). The possibility of such an “inverted merging” is not considered here.
When
2D vortices of the exactly shielded structure are brought into contact, their
cores merge while shell fluid is lost. However, if they have shell vorticity
greater than that given by (31)
(and consequently induce circulation around the edge of any arbitrarily large,
finite domain), their interaction in the presence of instability may cause
the shell fluid to merge while core fluid is rejected (Carton and Bertrand 1994
). The possibility of such an “inverted merging” is not considered here.
 5
5 A
third scenario was considered in which mass and energy were conserved. The
final state contained more angular momentum than the initial state, leading
us to reject this scenario as a physically meaningful description of free
vortex merging.
A
third scenario was considered in which mass and energy were conserved. The
final state contained more angular momentum than the initial state, leading
us to reject this scenario as a physically meaningful description of free
vortex merging.
 *
* School of Ocean and Earth Sciences and Technology, University of Hawaii Contribution Number 4897.
School of Ocean and Earth Sciences and Technology, University of Hawaii Contribution Number 4897.
 Corresponding author address: Dr. Pierre Flament, Department of Oceanography, University of Hawaii, 1000 Pope Road, Honolulu, HI 96822.
Corresponding author address: Dr. Pierre Flament, Department of Oceanography, University of Hawaii, 1000 Pope Road, Honolulu, HI 96822.
 E-mail: pflament@hawaii.edu
E-mail: pflament@hawaii.edu
![]() Mass,
angular momentum, and energy budgets are examined in an analytical model
of vortex merging relevant to midlatitude mesoscale eddies. The vortices
are baroclinic and cyclogeostrophic. The fluid surrounding them is assumed
to remain quiescent. It is shown that due to this surrounding fluid, angular
momentum is conserved when expressed in both the inertial and rotating frames
of reference.
Mass,
angular momentum, and energy budgets are examined in an analytical model
of vortex merging relevant to midlatitude mesoscale eddies. The vortices
are baroclinic and cyclogeostrophic. The fluid surrounding them is assumed
to remain quiescent. It is shown that due to this surrounding fluid, angular
momentum is conserved when expressed in both the inertial and rotating frames
of reference.![]() Lens-shaped solid-body vortices can conserve mass, angular momentum, and energy when they merge. If an upper-layer of thickness H1 is included in the model, the merged vortex must have either less energy or mass than the sum of the original two vortices.
Lens-shaped solid-body vortices can conserve mass, angular momentum, and energy when they merge. If an upper-layer of thickness H1 is included in the model, the merged vortex must have either less energy or mass than the sum of the original two vortices.![]() A
more complex model of the vortex azimuthal structure is then considered,
which includes a constant vorticity shell surrounding the solid-body core.
If the shell is large compared to the core, the mass, angular momentum, and
energy can all be conserved in the merged vortex. However, if the shell is
small, the merged vortex must have less energy or mass than in the solid-body
case.
A
more complex model of the vortex azimuthal structure is then considered,
which includes a constant vorticity shell surrounding the solid-body core.
If the shell is large compared to the core, the mass, angular momentum, and
energy can all be conserved in the merged vortex. However, if the shell is
small, the merged vortex must have less energy or mass than in the solid-body
case.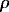 ) extends from z = 0 to z =
) extends from z = 0 to z =  H1 and the lower layer (density
H1 and the lower layer (density 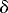

 (
( (r) to z =
(r) to z =  by cyclogeostrophy:
by cyclogeostrophy: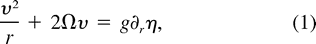

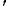 is g
is g (3)
(3)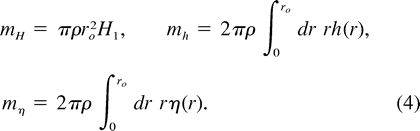

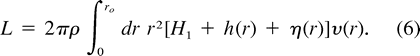
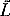 = L + MR2o
= L + MR2o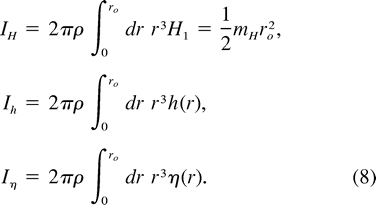

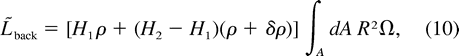
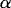 = 1, ·
= 1, · ·
·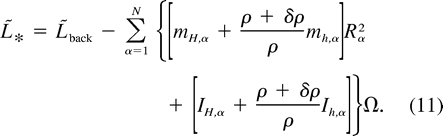
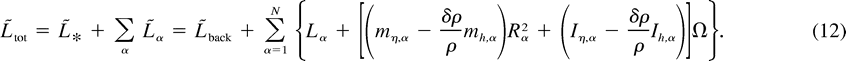
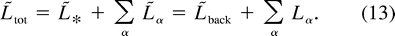
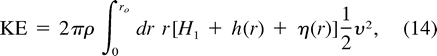
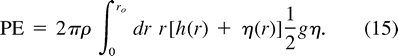
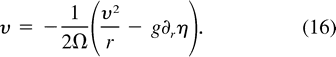
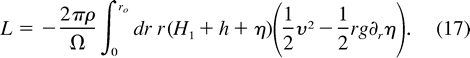
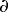 r
r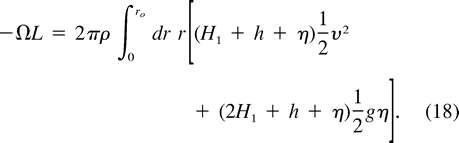
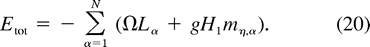
 r, where
r, where 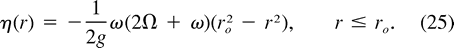
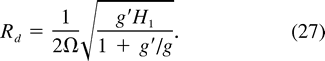
 0 or ra/Rd
0 or ra/Rd  , the vortices become anticyclonic lenses; in particular, zero potential vorticity lenses (
, the vortices become anticyclonic lenses; in particular, zero potential vorticity lenses (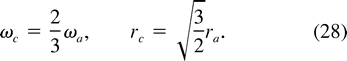
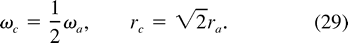
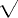 (2). For lens-shaped anticyclonic vortices (ra/Rd =
(2). For lens-shaped anticyclonic vortices (ra/Rd = 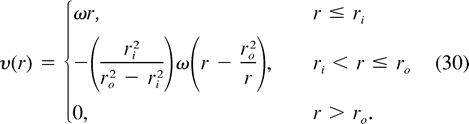
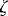 o to core vorticity
o to core vorticity 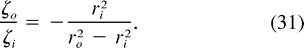
 ri, the outer shell is nearly irrotational and the vortex becomes Rankine-like. If ro <
ri, the outer shell is nearly irrotational and the vortex becomes Rankine-like. If ro < 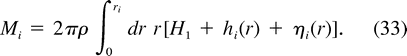
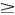 8, energy is conserved within 0.1% for all values of
8, energy is conserved within 0.1% for all values of 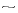 2) and inner and outer radii larger by
2) and inner and outer radii larger by 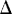 h, the underlying column must gain anticyclonic vorticity
h, the underlying column must gain anticyclonic vorticity 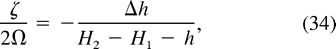
 . Later, they have merged to produce a single cylinder of the same density with mass mc = 2ma, radius rc, and rotation rate
. Later, they have merged to produce a single cylinder of the same density with mass mc = 2ma, radius rc, and rotation rate 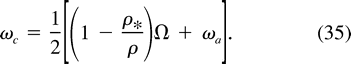
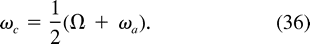



 .
.






