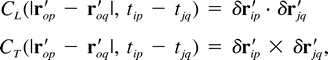© Copyright American Meteorological Society 2000
Journal of Physical Oceanography: Vol. 30, No. 1, pp. 51–66., 2000The Shear, Convergence, and Thermohaline Structure of a Front*
Pierre Flament
Department of Oceanography, School of Ocean and Earth Science and Technology, University of Hawaii at Manoa, Honolulu, Hawaii
Laurence Armi
Scripps Institution of Oceanography, University of California, San Diego, La Jolla, California
(Manuscript received 8 June 1998, 2 February 1999)
ABSTRACT With
the objective of measuring convergence directly to confirm previous observations
of frontal subduction, a seaward upwelling jet off central California was
studied using satellite infrared images, hydrographic sections, ship drift,
and clusters of surface drifters. The cyclonic front of the jet was sharper
than 1 km, resulting in a shear several times larger than f. A cross-frontal convergence of 7 cm s
With
the objective of measuring convergence directly to confirm previous observations
of frontal subduction, a seaward upwelling jet off central California was
studied using satellite infrared images, hydrographic sections, ship drift,
and clusters of surface drifters. The cyclonic front of the jet was sharper
than 1 km, resulting in a shear several times larger than f. A cross-frontal convergence of 7 cm s 1 over the width of the front (equivalent to 0.8f)
was visible as a 20-m-wide accumulation of debris. The sharpness of the front
lasted at least for a day. Away from the cyclonic front, the divergence of
the flow was small and the shear was less than 0.6f. Thermohaline
layers, originating at the front, were interleaving along isopycnals, suggesting
water subduction. It is proposed that the asymetry between anticyclonic and
cyclonic sides of the jet, and the strong convergence at the cyclonicfront,
resulted from a frictionally driven ageostrophic secondary circulation superimposed
on the geostrophic flow.
1 over the width of the front (equivalent to 0.8f)
was visible as a 20-m-wide accumulation of debris. The sharpness of the front
lasted at least for a day. Away from the cyclonic front, the divergence of
the flow was small and the shear was less than 0.6f. Thermohaline
layers, originating at the front, were interleaving along isopycnals, suggesting
water subduction. It is proposed that the asymetry between anticyclonic and
cyclonic sides of the jet, and the strong convergence at the cyclonicfront,
resulted from a frictionally driven ageostrophic secondary circulation superimposed
on the geostrophic flow.
TABLE OF CONTENTS
[1. Introduction] [2. Mesoscale structure...] [3. Velocity gradients] [4. Thermohaline structure] [5. Summary and...] [Appendix] [References] [Figures]
[Tables]
1. Introduction
 The
summertime mesoscale flow off central and northern California consists of
large meanders of the California Current. The seaward branches of these meanders
are narrow baroclinic jets, generally referred to as upwelling filaments,
and they flow along the offshore boundary of the freshly upwelled coastal
water. The cold temperature signature of these features was first observed
by Bernstein et al. (1977)
in satellite infrared images, and detailed in situ surveys of upwelling
filaments were first made in 1981 and 1982 off Point Arena 39°N, 124°W (Flament et al. 1985
; Kosro and Huyer 1986
; Rienecker et al. 1985
). The baroclinic jets have a width of 50 km, an offshore extension of up to 400 km, a maximum surface velocity of 80 cm s
The
summertime mesoscale flow off central and northern California consists of
large meanders of the California Current. The seaward branches of these meanders
are narrow baroclinic jets, generally referred to as upwelling filaments,
and they flow along the offshore boundary of the freshly upwelled coastal
water. The cold temperature signature of these features was first observed
by Bernstein et al. (1977)
in satellite infrared images, and detailed in situ surveys of upwelling
filaments were first made in 1981 and 1982 off Point Arena 39°N, 124°W (Flament et al. 1985
; Kosro and Huyer 1986
; Rienecker et al. 1985
). The baroclinic jets have a width of 50 km, an offshore extension of up to 400 km, a maximum surface velocity of 80 cm s 1 decreasing with a depth scale of 150 m, and a total offshore transport of about 2
1 decreasing with a depth scale of 150 m, and a total offshore transport of about 2 ·
· 106 m3 s
106 m3 s 1. The surface layer processes associated with these jets are often asymmetric. Flament et al. (1985)
found, at the anticyclonic boundary, a transition from cold to warm
water spread over 20 km but, at the cyclonic boundary, a front sharper than
1 km where water subduction was observed. Similar observations were made
subsequently during the 1987 Coastal Transition Zone experiment (Washburn et al. 1991
; Huyer et al. 1991
; Kosro et al. 1991
; Dewey et al. 1991
).
1. The surface layer processes associated with these jets are often asymmetric. Flament et al. (1985)
found, at the anticyclonic boundary, a transition from cold to warm
water spread over 20 km but, at the cyclonic boundary, a front sharper than
1 km where water subduction was observed. Similar observations were made
subsequently during the 1987 Coastal Transition Zone experiment (Washburn et al. 1991
; Huyer et al. 1991
; Kosro et al. 1991
; Dewey et al. 1991
).
 The
specific objectives of the observations reported here were to study the velocity
gradients associated with these fronts, resolving scales smaller than previously
possible, and to observe the distribution of thermohaline fine structure.
Satellite infrared images of sea surface temperature were used to guide the
R/V Sproul to a filament off Point Sur (36°30
The
specific objectives of the observations reported here were to study the velocity
gradients associated with these fronts, resolving scales smaller than previously
possible, and to observe the distribution of thermohaline fine structure.
Satellite infrared images of sea surface temperature were used to guide the
R/V Sproul to a filament off Point Sur (36°30 N,
122°W), which was surveyed between 17 and 29 July 1985. The mesoscale structure
of the filament, inferred from hydrographic stations, underway surface temperature
and salinity, and drifters tracks, is presented in section 2.
Measurements of velocity gradients and frontal convergence, using surface
drifters deployed in clusters and ship drift, are presented in section 3. The fine structure observed in the hydrographic stations and tow-yo CTD sections are described in section 4. These observations are summarized and interpreted in terms of surface layer processes in section 5.
The technique for measuring velocity gradients using clusters of drifters
is discussed in the appendix. Details about the other instruments and data
processing can be found in the appendix to Flament et al. (1985)
.
N,
122°W), which was surveyed between 17 and 29 July 1985. The mesoscale structure
of the filament, inferred from hydrographic stations, underway surface temperature
and salinity, and drifters tracks, is presented in section 2.
Measurements of velocity gradients and frontal convergence, using surface
drifters deployed in clusters and ship drift, are presented in section 3. The fine structure observed in the hydrographic stations and tow-yo CTD sections are described in section 4. These observations are summarized and interpreted in terms of surface layer processes in section 5.
The technique for measuring velocity gradients using clusters of drifters
is discussed in the appendix. Details about the other instruments and data
processing can be found in the appendix to Flament et al. (1985)
.
2. Mesoscale structure of the filament
 Two
24-h sequences of cloud-free satellite infrared images from the National
Oceanic and Atmospheric Administration (NOAA) polar orbiting satellites were
acquired, before the cruise on 8 and 9 July and after the cruise on 5 and
6 August. Marine stratus covered the area during most of the cruise, yielding
only a single usable image on 24 July. The images of 0300 UTC 9 July, 0300
UTC 24 July, and 1000 UTC 5 August are shown in Fig. 1
Two
24-h sequences of cloud-free satellite infrared images from the National
Oceanic and Atmospheric Administration (NOAA) polar orbiting satellites were
acquired, before the cruise on 8 and 9 July and after the cruise on 5 and
6 August. Marine stratus covered the area during most of the cruise, yielding
only a single usable image on 24 July. The images of 0300 UTC 9 July, 0300
UTC 24 July, and 1000 UTC 5 August are shown in Fig. 1  . A cold filament was rooted near 35°30
. A cold filament was rooted near 35°30 N, 122°W, meandering toward the southwest. Near 34°30
N, 122°W, meandering toward the southwest. Near 34°30 N,
123°W, it turned sharply to the southeast, following a persistent large-scale
zonal front. Its maximum offshore extension was 250 km. Small thermal features
with scales of 1 to 5 km, passively advected by the mesoscale flow, were
used to estimate surface velocities from the sequences of images. The cold
filament was the surface expression of a jet flowing offshore, with speeds
reaching at least 50 cm s
N,
123°W, it turned sharply to the southeast, following a persistent large-scale
zonal front. Its maximum offshore extension was 250 km. Small thermal features
with scales of 1 to 5 km, passively advected by the mesoscale flow, were
used to estimate surface velocities from the sequences of images. The cold
filament was the surface expression of a jet flowing offshore, with speeds
reaching at least 50 cm s 1.
1.
 The schedule of the ship survey is shown in Fig. 2
The schedule of the ship survey is shown in Fig. 2  .
The wind was upwelling-favorable during most of the survey, except during
two short relaxation events on 19 and 26 July. The positions of the CTD stations
relative to the boundaries of the filament on 24 July 1985 are shown in Fig. 3
.
The wind was upwelling-favorable during most of the survey, except during
two short relaxation events on 19 and 26 July. The positions of the CTD stations
relative to the boundaries of the filament on 24 July 1985 are shown in Fig. 3  .
The survey started on 20 July with a section to locate the jet, then proceeded
northward until 26 July, the section being repeated four times to detect
temporal variations of the flow.
.
The survey started on 20 July with a section to locate the jet, then proceeded
northward until 26 July, the section being repeated four times to detect
temporal variations of the flow.
 Mixed
layer drifters were deployed during the survey, either individually or in
clusters. Surface velocities were inferred from successive positions of these
drifters (Fig. 3
Mixed
layer drifters were deployed during the survey, either individually or in
clusters. Surface velocities were inferred from successive positions of these
drifters (Fig. 3  ); the median speed for the drifters deployed in the jet was 51 cm s
); the median speed for the drifters deployed in the jet was 51 cm s 1, consistent with the speed inferred from the sequences of satellite images (Fig. 1
1, consistent with the speed inferred from the sequences of satellite images (Fig. 1  ).
).
 Surface
temperature, salinity, geopotential anomaly referenced to 500 dbar, and a
contour plot of geostrophic velocity along the section made on 20 July are
displayed in Fig. 4
Surface
temperature, salinity, geopotential anomaly referenced to 500 dbar, and a
contour plot of geostrophic velocity along the section made on 20 July are
displayed in Fig. 4  .
Given the consistently southward direction followed by the drifters released
in the jet near the section, geostrophic velocity was computed assuming a
southward flow. Centripetal accelerations, estimated from the curvature of
the filament, were less than 20% of the Coriolis accelerations and were neglected.
The width of the jet was
.
Given the consistently southward direction followed by the drifters released
in the jet near the section, geostrophic velocity was computed assuming a
southward flow. Centripetal accelerations, estimated from the curvature of
the filament, were less than 20% of the Coriolis accelerations and were neglected.
The width of the jet was  30 km and its geostrophic transport referenced to 500 dbar was 2.0
30 km and its geostrophic transport referenced to 500 dbar was 2.0 ·
· 106 m3 s
106 m3 s 1. East of the jet, there was a weak northward geostrophic flow of
1. East of the jet, there was a weak northward geostrophic flow of  8 cm s
8 cm s 1. The flow was strongly surface intensified;the geostrophic velocity referenced to 500 dbar exceeded 90 cm s
1. The flow was strongly surface intensified;the geostrophic velocity referenced to 500 dbar exceeded 90 cm s 1 at the surface, but decreased to less than 20 cm s
1 at the surface, but decreased to less than 20 cm s 1 at 100-m depth (Fig. 5
1 at 100-m depth (Fig. 5  ); for reference, the velocity profile observed by Flament et al. (1985)
is also shown in Fig. 5
); for reference, the velocity profile observed by Flament et al. (1985)
is also shown in Fig. 5  (dashed). The large magnitude of surface velocity was confirmed by a drifter,
which, launched near the axis of the jet, averaged 84 cm s
(dashed). The large magnitude of surface velocity was confirmed by a drifter,
which, launched near the axis of the jet, averaged 84 cm s 1 southward over 6 hours.
1 southward over 6 hours.
 This filament and the filament repeatedly surveyed off Point Arena (Flament et al. 1985
; Kosro and Huyer 1986
; Rienecker et al. 1985
), appear to have very similar structures. Both corresponded to shallow
baroclinic jets transporting offshore a few Sverdrups of cold surface water,
bounded by warm and salty water on the cyclonic (southeastern side) and warm
and fresher water on the anticyclonic (northwestern) side. Both were surface
intensified, and both were associated with a shoreward flow on their cyclonic
side.
This filament and the filament repeatedly surveyed off Point Arena (Flament et al. 1985
; Kosro and Huyer 1986
; Rienecker et al. 1985
), appear to have very similar structures. Both corresponded to shallow
baroclinic jets transporting offshore a few Sverdrups of cold surface water,
bounded by warm and salty water on the cyclonic (southeastern side) and warm
and fresher water on the anticyclonic (northwestern) side. Both were surface
intensified, and both were associated with a shoreward flow on their cyclonic
side.
 Surface isotherms appear to converge toward the cyclonic front near 35°20
Surface isotherms appear to converge toward the cyclonic front near 35°20 N, 122°10
N, 122°10 W in the sequence of images from 9 July, enhanced and enlarged in Fig. 6
W in the sequence of images from 9 July, enhanced and enlarged in Fig. 6  . The distance between the front and a mushroom-shaped patch of cold water to the east, decreased from
. The distance between the front and a mushroom-shaped patch of cold water to the east, decreased from  14 to
14 to  8 km after 12 hours and to
8 km after 12 hours and to  5 km after 24 hours. Assuming the isotherms spacing to decrease as s = s0e
5 km after 24 hours. Assuming the isotherms spacing to decrease as s = s0e
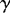 t, s being a cross-isotherm coordinate, a rough estimate of the convergence rate is
t, s being a cross-isotherm coordinate, a rough estimate of the convergence rate is 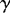
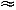 1.2
1.2 ·
· 10
10 5 s
5 s 1
1 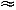 f/7 (all velocity gradients will be given in units of f = 8.6
f/7 (all velocity gradients will be given in units of f = 8.6 ×
× 10
10 5 s
5 s 1,
the planetary vorticity at this latitude). A cross-isotherm convergence toward
the cyclonic boundary was also inferred from satellite images by Flament et al. (1985)
.
1,
the planetary vorticity at this latitude). A cross-isotherm convergence toward
the cyclonic boundary was also inferred from satellite images by Flament et al. (1985)
.
 A
longitude/time contour of geopotential anomaly of the surface referenced
to 500 dbar along the repeated section reveals a westward translation of
the structure (Fig. 7
A
longitude/time contour of geopotential anomaly of the surface referenced
to 500 dbar along the repeated section reveals a westward translation of
the structure (Fig. 7  ).
Multiple linear regression of geopotential anomaly versus time and longitude
yields a translation speed to the west of 4.3 ± 0.7 cm s
).
Multiple linear regression of geopotential anomaly versus time and longitude
yields a translation speed to the west of 4.3 ± 0.7 cm s 1
(one standard deviation). This translation was also observed in the satellite
images: between 9 July and 5 August, the position at which the filament crossed
the 2000-m isobath, chosen to represent the shelf break, moved about 75 km
to the northwest, an average of 3.5 cm s
1
(one standard deviation). This translation was also observed in the satellite
images: between 9 July and 5 August, the position at which the filament crossed
the 2000-m isobath, chosen to represent the shelf break, moved about 75 km
to the northwest, an average of 3.5 cm s 1 (Fig. 1
1 (Fig. 1  ).
).
3. Velocity gradients
 Three
clusters of nine drifters each were deployed to directly measure the velocity
gradients at a scale of a few kilometers. Details of the experimental technique
and the estimation of the flow parameters are discussed in the appendix.
The positions of the clusters relative to the boundaries of the cold filament
observed in the image of 24 July are shown in Fig. 8
Three
clusters of nine drifters each were deployed to directly measure the velocity
gradients at a scale of a few kilometers. Details of the experimental technique
and the estimation of the flow parameters are discussed in the appendix.
The positions of the clusters relative to the boundaries of the cold filament
observed in the image of 24 July are shown in Fig. 8  . Cluster A spanned the sharp cyclonic front, cluster B was deployed near the axis of the cold filament, and cluster C
was deployed farther west on the anticyclonic side of the jet. The initial
grid spacing, the time and coordinates of the deployments, and the tracking
period of each cluster are given in Table 1
. Cluster A spanned the sharp cyclonic front, cluster B was deployed near the axis of the cold filament, and cluster C
was deployed farther west on the anticyclonic side of the jet. The initial
grid spacing, the time and coordinates of the deployments, and the tracking
period of each cluster are given in Table 1  .
As explained in the appendix, large horizontal strain limited the tracking
period of the clusters to a few hours, less than the tidal and inertial periods.
.
As explained in the appendix, large horizontal strain limited the tracking
period of the clusters to a few hours, less than the tidal and inertial periods.
 The trajectories of the drifters in cluster A, tracked for about 8 hours with an initial grid spacing of 2 km, are shown in Fig. 9
The trajectories of the drifters in cluster A, tracked for about 8 hours with an initial grid spacing of 2 km, are shown in Fig. 9  .
The flow was discontinuous at the spacing of the drifters; three drifters
moved rapidly southward in the jet, whereas most of the drifters east of
the jet moved slowly northwestward. The flow parameters, assuming slablike
motions on either side of the front, are listed in Table 1
.
The flow was discontinuous at the spacing of the drifters; three drifters
moved rapidly southward in the jet, whereas most of the drifters east of
the jet moved slowly northwestward. The flow parameters, assuming slablike
motions on either side of the front, are listed in Table 1  . The cyclonic shear
. The cyclonic shear  x
x across the front was larger than
across the front was larger than 
 /
/ x = 2.9f and there was a cross-frontal convergence
x = 2.9f and there was a cross-frontal convergence  xu stronger than
xu stronger than  u/
u/ x = 0.45f.
These are lower bounds because the width of the front was considerably less
than the spacing of the drifters. Surface salinity sampled while tracking
this cluster is shown in Fig. 9b
x = 0.45f.
These are lower bounds because the width of the front was considerably less
than the spacing of the drifters. Surface salinity sampled while tracking
this cluster is shown in Fig. 9b  ,
with light gray shades representing the high salinity warm water. The southward
jet corresponded to a transition from low salinity water (S = 32.9 psu) in the filament to high salinity water (S = 33.4 psu) to the east. Surface temperature variations were masked by intense diurnal warming (Flament et al. 1994
) and were therefore difficult to relate to the velocity front.
,
with light gray shades representing the high salinity warm water. The southward
jet corresponded to a transition from low salinity water (S = 32.9 psu) in the filament to high salinity water (S = 33.4 psu) to the east. Surface temperature variations were masked by intense diurnal warming (Flament et al. 1994
) and were therefore difficult to relate to the velocity front.
 A 20 m wide accumulation of debris, consisting of seaweeds such as Macrocystis pyrifera, ship refuse, sonobuoy containers, and bales of Canabis sativa, was found along the sharp front. A photograph of the accumulation of debris is shown in Fig. 10
A 20 m wide accumulation of debris, consisting of seaweeds such as Macrocystis pyrifera, ship refuse, sonobuoy containers, and bales of Canabis sativa, was found along the sharp front. A photograph of the accumulation of debris is shown in Fig. 10  . The drifters launched east of the jet were retrieved in this debris line, which extended straight from horizon to horizon at
. The drifters launched east of the jet were retrieved in this debris line, which extended straight from horizon to horizon at  190°
heading. The line was crossed repeatedly for several days (although its position
was only recorded on 26 and 27 July), and it migrated westward at
190°
heading. The line was crossed repeatedly for several days (although its position
was only recorded on 26 and 27 July), and it migrated westward at  6 cm s
6 cm s 1 (Fig. 10
1 (Fig. 10  , inset) following the translation of the jet (Fig. 9b
, inset) following the translation of the jet (Fig. 9b  is therefore not a truly synoptic view of the surface salinity field). No
other accumulation lines were observed during the cruise.
is therefore not a truly synoptic view of the surface salinity field). No
other accumulation lines were observed during the cruise.
 For
the purpose of detecting possible variations of water velocity across the
debris line, the ship was slowed down to a constant speed of 1.3 m s
For
the purpose of detecting possible variations of water velocity across the
debris line, the ship was slowed down to a constant speed of 1.3 m s 1
and steered on a constant gyrocompass heading orthogonal to the line. The
ship track crossing the line and entering the southward jet is shown in Fig. 11
1
and steered on a constant gyrocompass heading orthogonal to the line. The
ship track crossing the line and entering the southward jet is shown in Fig. 11  . Surface temperature, salinity, and density during the transect, also shown in Fig. 11
. Surface temperature, salinity, and density during the transect, also shown in Fig. 11  , confirm that the debris line coincided with the eastern boundary of the filament.
, confirm that the debris line coincided with the eastern boundary of the filament.
 Surface
currents, derived from the difference between velocity over ground using
LORAN-C and velocity over water using the electromagnetic log and the gyrocompass,
are given in Table 1
Surface
currents, derived from the difference between velocity over ground using
LORAN-C and velocity over water using the electromagnetic log and the gyrocompass,
are given in Table 1  . The alongfront flow varied from 2 cm s
. The alongfront flow varied from 2 cm s 1 east of the line to
1 east of the line to  64 cm s
64 cm s 1 in the jet, over a region 1 km wide starting at 122°30.5
1 in the jet, over a region 1 km wide starting at 122°30.5 W that ended at 122°31.5
W that ended at 122°31.5 W. The 1-km scale of the transition suggests a horizontal shear larger than 7.5f and a cross-frontal convergence stronger than 0.8f.
Closer examination of the track indicates that the transition may have been
concentrated over two very narrow regions barely resolved by the
W. The 1-km scale of the transition suggests a horizontal shear larger than 7.5f and a cross-frontal convergence stronger than 0.8f.
Closer examination of the track indicates that the transition may have been
concentrated over two very narrow regions barely resolved by the  80-m
sampling of the LORAN-C, implying even larger shear and converge rate. Unfortunately,
for all other crossings of the jet, the ship was steered with the LORAN-C
navigator on a constant track over ground, and gyrocompass heading was not
recorded. These other crossings cannot be used to infer subtle variations
of water velocity through the drift of the ship.
80-m
sampling of the LORAN-C, implying even larger shear and converge rate. Unfortunately,
for all other crossings of the jet, the ship was steered with the LORAN-C
navigator on a constant track over ground, and gyrocompass heading was not
recorded. These other crossings cannot be used to infer subtle variations
of water velocity through the drift of the ship.
 In contrast to the sharp front spanned by cluster A, the velocity field appeared continuous at clusters B and C,
varying over spatial scales larger than the span of the clusters and over
temporal scales longer than their tracking periods. The flow u(r, t) can therefore be approximated by a linearized Taylor series in the vicinity of some reference point r0:
In contrast to the sharp front spanned by cluster A, the velocity field appeared continuous at clusters B and C,
varying over spatial scales larger than the span of the clusters and over
temporal scales longer than their tracking periods. The flow u(r, t) can therefore be approximated by a linearized Taylor series in the vicinity of some reference point r0:
u(r) = u0 + 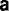 (r
(r  r0),
r0), (1)
(1)
where u0 = u(r0) is the mean velocity and 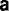 =
= 
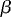 u
u is the second-order velocity gradient tensor. The drifter trajectories for clusters B and C are shown in Figs. 12
is the second-order velocity gradient tensor. The drifter trajectories for clusters B and C are shown in Figs. 12  and 13
and 13  , both in a fixed frame of reference and in a frame of reference translating with the mean velocity u0.
The corresponding flow parameters and standard deviation errors, estimated
using the procedure outlined in the appendix, are listed in Table 1
, both in a fixed frame of reference and in a frame of reference translating with the mean velocity u0.
The corresponding flow parameters and standard deviation errors, estimated
using the procedure outlined in the appendix, are listed in Table 1  .
. It is customary to decompose a velocity gradient tensor into an antisymmetrical part
It is customary to decompose a velocity gradient tensor into an antisymmetrical part 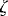

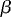 =
= 
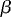 u
u


 u
u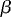 representing vorticity and a symmetrical part
representing vorticity and a symmetrical part 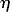

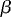 =
= 
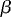 u
u +
+ 
 u
u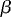 representing irrotational deformation, which can be further decomposed into an isotropic divergence Tr(
representing irrotational deformation, which can be further decomposed into an isotropic divergence Tr(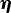 ) and a nondivergent strain,
) and a nondivergent strain, 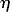


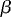 =
= 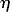

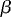
 Tr(
Tr(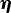 )
)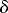

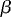 /2 (cf. Batchelor 1967
, p. 79). The eigenvectors of
/2 (cf. Batchelor 1967
, p. 79). The eigenvectors of 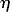


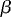 represent the principal axes of expansion and contraction. Such decomposition
of relative motion, of course, is not unique. Since the jet is approximately
a parallel shear flow, in which the mean velocity is an order of magnitude
larger than the velocity difference across the clusters, it is also useful
to decompose
represent the principal axes of expansion and contraction. Such decomposition
of relative motion, of course, is not unique. Since the jet is approximately
a parallel shear flow, in which the mean velocity is an order of magnitude
larger than the velocity difference across the clusters, it is also useful
to decompose 
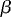 u
u into a pure shear parallel to the mean flow, an isotropic divergence, and a residual pure strain or confluence, as given in Table 1
into a pure shear parallel to the mean flow, an isotropic divergence, and a residual pure strain or confluence, as given in Table 1  .
.
 To interpret Table 1
To interpret Table 1  and summarize this section, the clusters and the ship crossing provided direct
measurements of the variations of horizontal shear across the filament: from
and summarize this section, the clusters and the ship crossing provided direct
measurements of the variations of horizontal shear across the filament: from
 0.6f on the anticyclonic side (A), to 1.2f near the axis (B), and to several times f at the cyclonic front (more than 2.9f from cluster A and more than 7.5f
from the ship drift). These astounding magnitudes of cyclonic vorticity can
be compared with the much smaller background vorticity of 0.05f inferred
25 km to the southeast of a filament rooted at the same location a year earlier
(see appendix). A cross-frontal convergence stronger than 0.8f was
observed at the cyclonic front, causing the accumulation of debris observed
repeatedly over several days. The alongfront gradients and thus total divergence
and residual strain could not be measured directly there, the cluster being
too rapidly elongated along the front to provide reliable estimates of
0.6f on the anticyclonic side (A), to 1.2f near the axis (B), and to several times f at the cyclonic front (more than 2.9f from cluster A and more than 7.5f
from the ship drift). These astounding magnitudes of cyclonic vorticity can
be compared with the much smaller background vorticity of 0.05f inferred
25 km to the southeast of a filament rooted at the same location a year earlier
(see appendix). A cross-frontal convergence stronger than 0.8f was
observed at the cyclonic front, causing the accumulation of debris observed
repeatedly over several days. The alongfront gradients and thus total divergence
and residual strain could not be measured directly there, the cluster being
too rapidly elongated along the front to provide reliable estimates of 
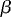 u
u .
.
 There was a small isotropic divergence of 0.3f near the axis (B),
suggesting that the cold anomaly may have been partially maintained by local
upwelling. There was also a small isotropic convergence of 0.3f on the anticyclonic side (C). A significant residual strain of 0.6f
was observed near the axis and on the anticyclonic side, with the diverging
principal direction of the strain oriented nearly parallel to the mean flow
within sampling errors at both locations, suggesting that the narrowness
of the filament may have been partially maintained by such confluence.
There was a small isotropic divergence of 0.3f near the axis (B),
suggesting that the cold anomaly may have been partially maintained by local
upwelling. There was also a small isotropic convergence of 0.3f on the anticyclonic side (C). A significant residual strain of 0.6f
was observed near the axis and on the anticyclonic side, with the diverging
principal direction of the strain oriented nearly parallel to the mean flow
within sampling errors at both locations, suggesting that the narrowness
of the filament may have been partially maintained by such confluence.
4. Thermohaline structure
 In
this section, CTD stations from the hydrographic survey along with tow-yo
sections at fine horizontal resolution will be used to discuss the thermohaline
structure in the neighborhood of the upwelling filament. It will be shown
that mixing at and beneath the jet was primarily along isopycnals, with sharp
subsurface fronts.
In
this section, CTD stations from the hydrographic survey along with tow-yo
sections at fine horizontal resolution will be used to discuss the thermohaline
structure in the neighborhood of the upwelling filament. It will be shown
that mixing at and beneath the jet was primarily along isopycnals, with sharp
subsurface fronts.
 The hydrographic stations can be grouped into four types (Fig. 14
The hydrographic stations can be grouped into four types (Fig. 14  ). For stations east of the filament (type“East”), salinity, from
). For stations east of the filament (type“East”), salinity, from  33.7 at the surface, varies little down to the 26.0 isopycnal at about 75-m depth. Beneath, salinity gradually increases to
33.7 at the surface, varies little down to the 26.0 isopycnal at about 75-m depth. Beneath, salinity gradually increases to  34
as the temperature further decreases to 6°C through the upper thermocline.
In contrast, for stations to the west of the filament (types “West” and “Far
West”), salinity first decreases from
34
as the temperature further decreases to 6°C through the upper thermocline.
In contrast, for stations to the west of the filament (types “West” and “Far
West”), salinity first decreases from  33
at the surface to a minimum of 32.8 on the 25.2 isopycnal at 50-m depth,
then rapidly increases to 33.7 on the 26.0 isopycnal, and finally follows
at greater depths the same T–S relationship as stations to
the east. The stations immediately to the west of the front (type “West”)
differ slightly between the 25.3 and 26.0 isopycnals from stations farther
to the west (type “Far West”), possibly reflecting a different upstream origin
of this deeper water, but the overall structure of the water column is similar.
33
at the surface to a minimum of 32.8 on the 25.2 isopycnal at 50-m depth,
then rapidly increases to 33.7 on the 26.0 isopycnal, and finally follows
at greater depths the same T–S relationship as stations to
the east. The stations immediately to the west of the front (type “West”)
differ slightly between the 25.3 and 26.0 isopycnals from stations farther
to the west (type “Far West”), possibly reflecting a different upstream origin
of this deeper water, but the overall structure of the water column is similar.
 Profiles
characterized by multiple thermohaline inversions are found in the vicinity
of the cyclonic front, suggesting strong interleaving at the boundary between
the two extreme water column types (shown as“Mixed” in Fig. 14c
Profiles
characterized by multiple thermohaline inversions are found in the vicinity
of the cyclonic front, suggesting strong interleaving at the boundary between
the two extreme water column types (shown as“Mixed” in Fig. 14c  ). The vertical scale of the interleaving is typically 10 to 20 m, with little spatial correlation between neighboring stations.
). The vertical scale of the interleaving is typically 10 to 20 m, with little spatial correlation between neighboring stations.
 To
gain more insight into the relationship between the thermohaline inversions
and the front, two CTD tow-yo sections were conducted across the filament,
one near where the clusters were deployed, the other about 50 km upstream,
closer to the root (Fig. 15
To
gain more insight into the relationship between the thermohaline inversions
and the front, two CTD tow-yo sections were conducted across the filament,
one near where the clusters were deployed, the other about 50 km upstream,
closer to the root (Fig. 15  ). The temperature and salinity fields are shown in Fig. 16
). The temperature and salinity fields are shown in Fig. 16  , with the isopycnals overlaid.
, with the isopycnals overlaid.
 Both
sections reveal a strong subsurface front spanning the 25.0 to 26.0 isopycnals,
separating warmer and more saline waters to the east from colder and fresher
waters to the west. Thermohaline intrusions are observed along isopycnals,
interleaving away from the subsurface front at
Both
sections reveal a strong subsurface front spanning the 25.0 to 26.0 isopycnals,
separating warmer and more saline waters to the east from colder and fresher
waters to the west. Thermohaline intrusions are observed along isopycnals,
interleaving away from the subsurface front at  122°45
122°45 W,
mostly in the northern section. On any isopycnal, the transition between
the two water column types is abrupt, barely resolved by the
W,
mostly in the northern section. On any isopycnal, the transition between
the two water column types is abrupt, barely resolved by the  500 m horizontal resolution of the tow-yo.
500 m horizontal resolution of the tow-yo.
 Above the 25.0 isopycnal, the T–S
relationships on both sides of the front are affected by intense diurnal
surface warming, a result of the slack winds observed during the tow-yos
on 25 to 27 July (Fig. 2
Above the 25.0 isopycnal, the T–S
relationships on both sides of the front are affected by intense diurnal
surface warming, a result of the slack winds observed during the tow-yos
on 25 to 27 July (Fig. 2  ). These warming events are seen as thin 13° to 16°C layers, extending from the surface to a sharp thermocline at
). These warming events are seen as thin 13° to 16°C layers, extending from the surface to a sharp thermocline at  10
m depth. There is no evidence of a well-mixed surface layer, and no corresponding
halocline. The warm surface layers appear to be interrupted near the axis
of the jet, where colder water at 12.5°C outcrops, possibly confirming the
divergence sampled by cluster B in this part of the jet. Although
the surface warming masks the temperature front, the convergence is nevertheless
observable at the surface, as evidenced by the debris line shown in Fig. 10
10
m depth. There is no evidence of a well-mixed surface layer, and no corresponding
halocline. The warm surface layers appear to be interrupted near the axis
of the jet, where colder water at 12.5°C outcrops, possibly confirming the
divergence sampled by cluster B in this part of the jet. Although
the surface warming masks the temperature front, the convergence is nevertheless
observable at the surface, as evidenced by the debris line shown in Fig. 10  .
.
 Our interpretation of the overall thermohaline structure of the filament is summarized by Fig. 17
Our interpretation of the overall thermohaline structure of the filament is summarized by Fig. 17  , showing the median T–S profile of each water column type observed. Slicing off an
, showing the median T–S profile of each water column type observed. Slicing off an  20 m deep surface layer affected by diurnal warming, the remaining T–S configuration is reminiscent of that observed by Flament et al. (1985)
off northern California. To the east of the filament, warm saline water
is found on the 25.7 isopycnal and below. As one progresses westward at constant
density, this layer becomes deeper and is capped by a layer of colder and
less saline water. However, the horizontal extent of the subducted layer—limited
by the subsurface front—is much shorter than observed by Flament et al. (1985)
, that is, a few kilometers versus a few tens of kilometers. The large
low salinity inversion found at depth 80 to 120 m farther west appears to
originate at the root of the filament nearshore, rather than result from
a cross-frontal subduction.
20 m deep surface layer affected by diurnal warming, the remaining T–S configuration is reminiscent of that observed by Flament et al. (1985)
off northern California. To the east of the filament, warm saline water
is found on the 25.7 isopycnal and below. As one progresses westward at constant
density, this layer becomes deeper and is capped by a layer of colder and
less saline water. However, the horizontal extent of the subducted layer—limited
by the subsurface front—is much shorter than observed by Flament et al. (1985)
, that is, a few kilometers versus a few tens of kilometers. The large
low salinity inversion found at depth 80 to 120 m farther west appears to
originate at the root of the filament nearshore, rather than result from
a cross-frontal subduction.
5. Summary and discussion
 Through
a small-scale sampling of the velocity structure of a seaward filament rooted
off central California, we have inferred that 1) the cyclonic front of the
filament was sharper than 1 km, resulting in a horizontal shear that reached
several times f; 2) elsewhere, the shear was less than 0.6f; 3) a cross-frontal convergence
Through
a small-scale sampling of the velocity structure of a seaward filament rooted
off central California, we have inferred that 1) the cyclonic front of the
filament was sharper than 1 km, resulting in a horizontal shear that reached
several times f; 2) elsewhere, the shear was less than 0.6f; 3) a cross-frontal convergence  7 cm s
7 cm s 1 over less than 1 km (larger than 0.8f)
was visible as a 20 m wide accumulation of debris coinciding with the cyclonic
front; 4) elsewhere, the divergence was small; and (5) the sharp front persisted
at least for a day—a period much longer than the timescale corresponding
to the vorticity (i.e., 2
1 over less than 1 km (larger than 0.8f)
was visible as a 20 m wide accumulation of debris coinciding with the cyclonic
front; 4) elsewhere, the divergence was small; and (5) the sharp front persisted
at least for a day—a period much longer than the timescale corresponding
to the vorticity (i.e., 2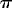 /7.5f
= 2.7 h). The asymmetry between the cyclonic and anticyclonic sides of the
jet and the very large cyclonic shears are consistent with the findings of
Flament et al. (1985)
, but has now been observed at higher resolution, with the shear and
convergence rates being measured directly with surface drifters, not just
indirectly from satellite images.
/7.5f
= 2.7 h). The asymmetry between the cyclonic and anticyclonic sides of the
jet and the very large cyclonic shears are consistent with the findings of
Flament et al. (1985)
, but has now been observed at higher resolution, with the shear and
convergence rates being measured directly with surface drifters, not just
indirectly from satellite images.
 Very sharp convergent shear fronts associated with upwelling filaments have been reported by others. Aside from Sheres et al. (1985)
, who inferred a shear of
Very sharp convergent shear fronts associated with upwelling filaments have been reported by others. Aside from Sheres et al. (1985)
, who inferred a shear of  10f from swell refraction seen in an image taken from aircraft, Moum et al. (1990)
found a convergent slick, observed as a thickening of the surface microlayer,
coinciding almost exactly with the temperature front of a filament off Point
Arena. Very similar to our observations were the measurements of Sanford et al. (1988)
. Using a towed geomagnetic electro-kinetograph, they measured relative vorticities reaching 6.5f at the southern boundary of a filament off Cape Mendocino, but only
10f from swell refraction seen in an image taken from aircraft, Moum et al. (1990)
found a convergent slick, observed as a thickening of the surface microlayer,
coinciding almost exactly with the temperature front of a filament off Point
Arena. Very similar to our observations were the measurements of Sanford et al. (1988)
. Using a towed geomagnetic electro-kinetograph, they measured relative vorticities reaching 6.5f at the southern boundary of a filament off Cape Mendocino, but only  0.5 to
0.5 to  1f
near the northern boundary. The velocity signature was entirely baroclinic
with no detectable barotropic shear. There is therefore a consistent set
of observations suggesting that sharp convergent shear fronts may be a general
feature of upwelling filaments.
1f
near the northern boundary. The velocity signature was entirely baroclinic
with no detectable barotropic shear. There is therefore a consistent set
of observations suggesting that sharp convergent shear fronts may be a general
feature of upwelling filaments.
 The
subsurface temperature and salinity fields reflected this cross-frontal circulation.
Although details of the thermohaline structure depend on many factors, including
the specific T–S relationships of the upstream source waters and the effects along the offshore advection path of wind stress (the case of Flament et al. 1985
) or heat flux (this experiment) on the surface layer, isopycnal interleaving suggestive of subducted layers, and sharp O(100 m) thermohaline fronts, have been consistently observed.
The
subsurface temperature and salinity fields reflected this cross-frontal circulation.
Although details of the thermohaline structure depend on many factors, including
the specific T–S relationships of the upstream source waters and the effects along the offshore advection path of wind stress (the case of Flament et al. 1985
) or heat flux (this experiment) on the surface layer, isopycnal interleaving suggestive of subducted layers, and sharp O(100 m) thermohaline fronts, have been consistently observed.
 Mechanisms
that may force the observed convergences fall in two categories: those resulting
from cross-frontal variation of the wind-driven Ekman transport, and those
resulting strictly from oceanic processes. A straight two-dimensional jet
flowing westward (U(y) < 0) will be assumed, y being the cross-front coordinate.
Mechanisms
that may force the observed convergences fall in two categories: those resulting
from cross-frontal variation of the wind-driven Ekman transport, and those
resulting strictly from oceanic processes. A straight two-dimensional jet
flowing westward (U(y) < 0) will be assumed, y being the cross-front coordinate.
 For a slablike mixed layer, the cross-frontal depth-averaged generalized Ekman velocity is
For a slablike mixed layer, the cross-frontal depth-averaged generalized Ekman velocity is
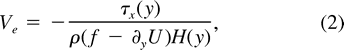
where the effect of the vorticity of the horizontal shear 
 yU has been included through the nonlinear term of the momentum balance (Stern 1975
). Cross-frontal variations of
yU has been included through the nonlinear term of the momentum balance (Stern 1975
). Cross-frontal variations of  , U, or H induce variations of Ve, thus Ekman convergence/divergence. Specifically:
, U, or H induce variations of Ve, thus Ekman convergence/divergence. Specifically:A change of the drag coefficient CD, hence of  , results from variations of the air–sea temperature difference (Businger and Shaw 1984
; Hanson 1987
). For a column of air initially in thermal equilibrium with water, reaching a 1.5°C front, CD varies by
, results from variations of the air–sea temperature difference (Businger and Shaw 1984
; Hanson 1987
). For a column of air initially in thermal equilibrium with water, reaching a 1.5°C front, CD varies by  25% at 2 m s
25% at 2 m s 1 and
1 and  15% at 5 m s
15% at 5 m s 1 (Smith 1988
). This effect decreases rapidly as the wind speed increases. In the
Northern Hemisphere, Ekman convergence occurs where colder water is to the
right of the wind.
1 (Smith 1988
). This effect decreases rapidly as the wind speed increases. In the
Northern Hemisphere, Ekman convergence occurs where colder water is to the
right of the wind.
Since the local vorticity  yU varies across the jet, the magnitude of Ve decreases on the cyclonic side and is enhanced on the anticyclonic side. Ekman convergence results when
yU varies across the jet, the magnitude of Ve decreases on the cyclonic side and is enhanced on the anticyclonic side. Ekman convergence results when  x
x yyU > 0, or along the axis for a westerly wind blowing against a westward jet (Niiler 1969
; cf. also Stern 1975
). For shear variations of order f, order 1 variations of the Ekman transport result, consistent with the convergence rates observed.
yyU > 0, or along the axis for a westerly wind blowing against a westward jet (Niiler 1969
; cf. also Stern 1975
). For shear variations of order f, order 1 variations of the Ekman transport result, consistent with the convergence rates observed.
Variations of H may result from different deepening histories
of the mixed layers on either side of a front, having been advected from
different origins, and their deepening having been modulated by the varying
horizontal shear (Klein and LeSaos 1986
). Ekman convergence is induced where  x
x yH < 0.
yH < 0.
 Although
these wind-driven processes are certainly able to force convergences, they
cannot alone explain the consistent asymmetry of the filaments: sharp fronts
have always been observed on the cyclonic side of the offhsore-flowing jets,
yet a change of sign of
Although
these wind-driven processes are certainly able to force convergences, they
cannot alone explain the consistent asymmetry of the filaments: sharp fronts
have always been observed on the cyclonic side of the offhsore-flowing jets,
yet a change of sign of  in (2) would permute convergent and divergent regions. Could an oceanic process independent of the wind be invoked?
in (2) would permute convergent and divergent regions. Could an oceanic process independent of the wind be invoked?
 The convergence may indeed be a secondary frictional flow Vf induced by the alongfront geostrophic flow Ug:
The convergence may indeed be a secondary frictional flow Vf induced by the alongfront geostrophic flow Ug:
fVf = 

 2zzUg,
2zzUg, (3)
(3)
where horizontal friction has been neglected. Assuming an exponential velocity profile Ug = U0(y)e z/z0 with z0
z/z0 with z0 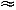 65 m (cf. Fig. 5
65 m (cf. Fig. 5  ), the frictionally driven secondary circulation is
), the frictionally driven secondary circulation is
where 
 is the vertical eddy viscosity. A convergence over the cyclonic region results. For a typical upper ocean where
is the vertical eddy viscosity. A convergence over the cyclonic region results. For a typical upper ocean where 
 = 0.1 m2 s
= 0.1 m2 s 1, the convergence induced by a shear of 3f would be about f. It would not be confined to the wind-driven layer.
1, the convergence induced by a shear of 3f would be about f. It would not be confined to the wind-driven layer. Clearly,
several processes may contribute to force the convergence, some playing a
dominant role in low wind conditions (this paper; Moum et al. 1990
) and others in high wind conditions (Flament et al. 1985
; Sheres et al. 1985
; Sanford et al. 1988
). Although the data presently available are not sufficient to single
any out, the frictional effect on the mean flow has the appeal of universality.
It yields an intriguingly simple scale for the width of surface and subsurface
fronts in advective–diffusive balance. The equilibrium width of such fronts
is (Thorpe 1983
)
Clearly,
several processes may contribute to force the convergence, some playing a
dominant role in low wind conditions (this paper; Moum et al. 1990
) and others in high wind conditions (Flament et al. 1985
; Sheres et al. 1985
; Sanford et al. 1988
). Although the data presently available are not sufficient to single
any out, the frictional effect on the mean flow has the appeal of universality.
It yields an intriguingly simple scale for the width of surface and subsurface
fronts in advective–diffusive balance. The equilibrium width of such fronts
is (Thorpe 1983
)
l = 2( h/
h/ yV)1/2.
yV)1/2. (5)
(5)
Combining (4) and (5) and defining Ro =  yU/f,l = 2(
yU/f,l = 2( h/
h/
 )1/2Ro
)1/2Ro 1/2z0,
1/2z0,
which
suggests that, regardless of the details of the flow field, fronts with widths
scaling with the thermocline depth are bound to form in regions of very large
cyclonic horizontal shear. Acknowledgments. Precise maneuvers by L. Zimm, master of the R/V E. B. Scripps in 1984, and by T. Beattie, master of the R/V R. G. Sproul
in 1985, made tracking the drifters possible. D. Chester, L. Christel, M.
Crawford, R. Olsen, S. Taylor, C. Trefois, and S. Yamasaki helped with the
operations at sea. M. Sawyer prepared the figures using the plotting package
gri by D. Kelley. R. Hansen, S. Laurent, and S. Laurent helped clarify
the cluster bootstrapping procedure. R. Hall gave insightful comments on
the effects of friction. This work was supported by the Office of Naval Research
(Contracts N000014-80-C-0440, N00014-87-K-007, N00014-96-1-0411).
Acknowledgments. Precise maneuvers by L. Zimm, master of the R/V E. B. Scripps in 1984, and by T. Beattie, master of the R/V R. G. Sproul
in 1985, made tracking the drifters possible. D. Chester, L. Christel, M.
Crawford, R. Olsen, S. Taylor, C. Trefois, and S. Yamasaki helped with the
operations at sea. M. Sawyer prepared the figures using the plotting package
gri by D. Kelley. R. Hansen, S. Laurent, and S. Laurent helped clarify
the cluster bootstrapping procedure. R. Hall gave insightful comments on
the effects of friction. This work was supported by the Office of Naval Research
(Contracts N000014-80-C-0440, N00014-87-K-007, N00014-96-1-0411).
APPENDIX
Measuring Velocity Gradients
 We present the technique used for measuring the surface velocity gradient tensor
We present the technique used for measuring the surface velocity gradient tensor 
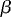 u
u at a scale of a few kilometers, using clusters of drifting buoys tracked for a few hours. Measurements of
at a scale of a few kilometers, using clusters of drifting buoys tracked for a few hours. Measurements of 
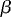 u
u at the surface are not new: examples based on triads of drifters can be found in Reed (1971)
, Chew and Berberian (1971)
, Molinari and Kirwan (1975)
, Kirwan (1975)
, and more recently in Niiler et al. (1989)
. Here, we used a larger number of drifters, allowing better estimation of standard errors.
at the surface are not new: examples based on triads of drifters can be found in Reed (1971)
, Chew and Berberian (1971)
, Molinari and Kirwan (1975)
, Kirwan (1975)
, and more recently in Niiler et al. (1989)
. Here, we used a larger number of drifters, allowing better estimation of standard errors.
 The subsurface drifter introduced by Davis (1985)
, minimizing the rectification of wave forces and the wind drag, was
used. It consists of a radio beacon connected to a drogue by a polyamide
line. A flashing light was attached to the antenna to assist in tracking.
In a preliminary test, large vertical shears caused the original dihedral
drogues to kite and the line to be pulled up to 60° from the vertical (i.e.,
the drogue was subject to a lift force instead of a pure drag). A fifth sail
was therefore added to prevent lift, closing the lower face of the dihedral
angle.
The subsurface drifter introduced by Davis (1985)
, minimizing the rectification of wave forces and the wind drag, was
used. It consists of a radio beacon connected to a drogue by a polyamide
line. A flashing light was attached to the antenna to assist in tracking.
In a preliminary test, large vertical shears caused the original dihedral
drogues to kite and the line to be pulled up to 60° from the vertical (i.e.,
the drogue was subject to a lift force instead of a pure drag). A fifth sail
was therefore added to prevent lift, closing the lower face of the dihedral
angle.
 Drifters
were deployed in clusters of nine on a 3 by 3 square grid with a grid spacing
of 1 to 4 km and tracked while the seeded parcel of water was advected and
deformed by the mesoscale flow. They were tracked by homing the ship successively
to each drifter, resulting in a set of nonsynchronous positions every 2 to
5 hours. A LORAN-C receiver was used for navigation. Random position errors
were estimated to be 70 m in latitude and 100 m in longitude.
Drifters
were deployed in clusters of nine on a 3 by 3 square grid with a grid spacing
of 1 to 4 km and tracked while the seeded parcel of water was advected and
deformed by the mesoscale flow. They were tracked by homing the ship successively
to each drifter, resulting in a set of nonsynchronous positions every 2 to
5 hours. A LORAN-C receiver was used for navigation. Random position errors
were estimated to be 70 m in latitude and 100 m in longitude.
 The following notations will be used: rip is the ith position on drifter p taken at time tip,
The following notations will be used: rip is the ith position on drifter p taken at time tip,  rip = ri+1p
rip = ri+1p  rip is the displacement of drifter p during the interval
rip is the displacement of drifter p during the interval  tip = ti+1p
tip = ti+1p  tip, and
tip, and 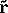 ip = (rip + ri+1p)/2 is the mean position of the drifter during that interval.
ip = (rip + ri+1p)/2 is the mean position of the drifter during that interval.
 Away from fronts, the mesoscale velocity field u(r,
Away from fronts, the mesoscale velocity field u(r, t)
is assumed to vary over a temporal scale longer than the inertial period
and over a spatial scale larger than the internal radius of deformation,
typically 30 km for the midlatitude eastern Pacific (Emery et al. 1984
). The clusters were much smaller, and were tracked for an inertial period or less. The value u(r) can therefore be approximated by a Taylor series limited to first order:
t)
is assumed to vary over a temporal scale longer than the inertial period
and over a spatial scale larger than the internal radius of deformation,
typically 30 km for the midlatitude eastern Pacific (Emery et al. 1984
). The clusters were much smaller, and were tracked for an inertial period or less. The value u(r) can therefore be approximated by a Taylor series limited to first order:
u(r) = u0 + 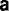 (r
(r  r0),
r0),
where u0 = u(r0) is the mean velocity, 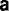 =
= 
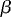 u
u is the 2 × 2 velocity gradient tensor, and r0
is a reference point in the immediate vicinity of the cluster. At this approximation,
the trajectory of a particle is governed bydtr = u0 +
is the 2 × 2 velocity gradient tensor, and r0
is a reference point in the immediate vicinity of the cluster. At this approximation,
the trajectory of a particle is governed bydtr = u0 + 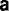 (r
(r  r0).
r0). (A1)
(A1)
The solutions of this differential system depend on the eigenvalues of  , involving exponentials of t if they are real, multiplied by sine and cosine of t if they are complex, and by linear terms in t if they are equal. Estimating u0 and
, involving exponentials of t if they are real, multiplied by sine and cosine of t if they are complex, and by linear terms in t if they are equal. Estimating u0 and  by minimizing the mean square position error on the Lagrangian trajectories
would require solving a nonlinear problem, the analytical form of which depends
unfortunately on the solution itself. The complication of a nonlinear estimator
is not justified here because the mesoscale deformation field was homogeneous
at the scale of the clusters.
by minimizing the mean square position error on the Lagrangian trajectories
would require solving a nonlinear problem, the analytical form of which depends
unfortunately on the solution itself. The complication of a nonlinear estimator
is not justified here because the mesoscale deformation field was homogeneous
at the scale of the clusters. We used instead a simple linear pseudo Eulerian model based on a centered first difference approximation of (A1):
We used instead a simple linear pseudo Eulerian model based on a centered first difference approximation of (A1):
 rip = u0
rip = u0 tip +
tip +  (
(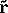 ip
ip  r0)
r0) tip +
tip +  r
r ip,
ip, (A2)
(A2)
where  r
r ip
are residuals due to unresolved small-scale processes, inhomogeneities of
the deformation field, and random position errors. The reference point r0 was chosen at the weighted mean drifters position
ip
are residuals due to unresolved small-scale processes, inhomogeneities of
the deformation field, and random position errors. The reference point r0 was chosen at the weighted mean drifters position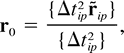
where
braces denote an average over the set of pairs of successive positions of
all the drifters. The origin of coordinates was then set at r0. Note that u0 depends on the choice of the reference point r0 [with respect to another point r1, u1 = u0 + 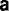 (r1
(r1  r0)], but that, to first order,
r0)], but that, to first order, 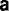 does not.
does not. Minimization of the residual variance {|
Minimization of the residual variance {| r
r ip|2} yields normal equations for u0 and
ip|2} yields normal equations for u0 and 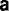 = [a
= [a
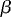 ]:
]:
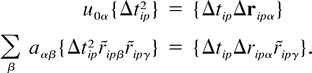
This model differs slightly from the technique of Okubo and Ebbesmeyer (1976)
and Molinari and Kirwan (1975)
: because the sampling interval was not constant, first differences  rip rather than velocities
rip rather than velocities  rip/
rip/ tip were used to avoid larger errors associated with small values of
tip were used to avoid larger errors associated with small values of  tip; because the drifters were not tracked synchronously, only the average tensor
tip; because the drifters were not tracked synchronously, only the average tensor 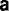 was estimated.
was estimated. The expression for the variance of the parameters of a minimum mean square error model yields (cf. Meyer 1975
):
The expression for the variance of the parameters of a minimum mean square error model yields (cf. Meyer 1975
):
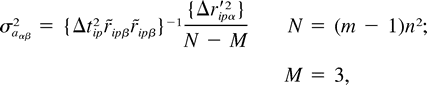
where N is the number of data points and M is the number of estimated parameters (1 velocity + 2 gradient) per component, n2 is the number of drifters, and m is the number of positions on each drifter. Assuming that the residual displacements  r
r ip
ip are uncorrelated with stationary and homogeneous statistics, the covariance matrix can be approximated as
are uncorrelated with stationary and homogeneous statistics, the covariance matrix can be approximated as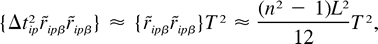
where L is the mean grid spacing of the n × n cluster and T is the mean sampling interval. The standard error 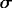 a
a
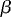 is then
is then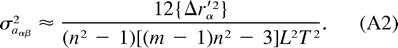
 Alternately, standard errors on u0 and
Alternately, standard errors on u0 and  can be obtained by a stochastic procedure, in which the configuration of
the sampling cluster is varied randomly while statistics of the estimated
parameters are collected (a so-called “bootstrap,” Efron and Gong 1983
; see, also, D’Asaro 1985
; Kunze and Sanford 1986
). Randomly resampled clusters were constructed by drawing with replacement n × n
drifters out of the original cluster, allowing duplications and omissions
(limited to two to prevent the generation of singular clusters). The parameters
were then estimated from the original positions on each resampled cluster,
and the probability density functions and standard deviations of the parameters
computed.
can be obtained by a stochastic procedure, in which the configuration of
the sampling cluster is varied randomly while statistics of the estimated
parameters are collected (a so-called “bootstrap,” Efron and Gong 1983
; see, also, D’Asaro 1985
; Kunze and Sanford 1986
). Randomly resampled clusters were constructed by drawing with replacement n × n
drifters out of the original cluster, allowing duplications and omissions
(limited to two to prevent the generation of singular clusters). The parameters
were then estimated from the original positions on each resampled cluster,
and the probability density functions and standard deviations of the parameters
computed.
 The
technique was tested in 1984. Satellite thermal infrared images were used
to guide the ship away from large horizontal velocity gradients. The cluster
was deployed in an isothermal region, 25 km to the southeast of the cold
filament originating near Point Sur (36°30
The
technique was tested in 1984. Satellite thermal infrared images were used
to guide the ship away from large horizontal velocity gradients. The cluster
was deployed in an isothermal region, 25 km to the southeast of the cold
filament originating near Point Sur (36°30 N,
122°W), in water 3000 m deep. Hydrographic stations showed a 20-m-deep mixed
layer, which remained at a constant temperature of 16°C while the cluster
was tracked. The drifters were drogued at half the mixed layer depth.
N,
122°W), in water 3000 m deep. Hydrographic stations showed a 20-m-deep mixed
layer, which remained at a constant temperature of 16°C while the cluster
was tracked. The drifters were drogued at half the mixed layer depth.
 The spacing of the drifters was
The spacing of the drifters was  4.5 km; a set of positions was obtained every 5 h for about 24 h (Fig. A1
4.5 km; a set of positions was obtained every 5 h for about 24 h (Fig. A1  ). The drifters moved westward at a nearly uniform speed of 24 cm s
). The drifters moved westward at a nearly uniform speed of 24 cm s 1. The estimated flow parameters are given in Table A1
1. The estimated flow parameters are given in Table A1  , with standard errors determined from 104 bootstrap realizations. The standard error computed from (A2) is 2.4
, with standard errors determined from 104 bootstrap realizations. The standard error computed from (A2) is 2.4 ·
· 10
10 6 s
6 s 1, similar to the bootstrap errors. The velocity gradient corresponded to a weak but significant positive vorticity (a21
1, similar to the bootstrap errors. The velocity gradient corresponded to a weak but significant positive vorticity (a21  a12) = 4.3
a12) = 4.3 ×
× 10
10 6 s
6 s 1
1  f/20. Figure A2
f/20. Figure A2  shows the trajectories in the absolute frame of reference, and in the frame of reference translating with the mean flow u0. The weak vorticity is noticeable (cf. drifters 8 with 4, or 6 with 2).
shows the trajectories in the absolute frame of reference, and in the frame of reference translating with the mean flow u0. The weak vorticity is noticeable (cf. drifters 8 with 4, or 6 with 2).
 The rms residual displacement {|
The rms residual displacement {| r
r ip|2}1/2,
unexplained by the model, is about 750 m for each component, larger than
the LORAN-C position error. Several processes may contribute to these residuals.
The model of Pollard and Millard (1970)
predicts wind-driven inertial oscillations of
ip|2}1/2,
unexplained by the model, is about 750 m for each component, larger than
the LORAN-C position error. Several processes may contribute to these residuals.
The model of Pollard and Millard (1970)
predicts wind-driven inertial oscillations of  2 cm s
2 cm s 1,
corresponding to a gyration radius of 240 m. Typical amplitudes for the semidiurnal
tide and the diurnal tide off California are 4 and 1 cm s
1,
corresponding to a gyration radius of 240 m. Typical amplitudes for the semidiurnal
tide and the diurnal tide off California are 4 and 1 cm s 1 (Noble et al. 1986
; Munk et al. 1970
), corresponding to displacements of 280 and 140 m. The rms horizontal
displacement due to the internal wave continuum, modeled by the canonical
GM-79 spectrum extrapolated to the surface (Munk et al. 1981
), is 420 m for each component. Incoherently adding these variances
gives rms residuals of 520 m for each component, in fair agreement with the
observed residuals. Drifters may also be entrained in Langmuir cells, often
associated with down-wind jets (Weller et al. 1985
), further increasing the residuals.
1 (Noble et al. 1986
; Munk et al. 1970
), corresponding to displacements of 280 and 140 m. The rms horizontal
displacement due to the internal wave continuum, modeled by the canonical
GM-79 spectrum extrapolated to the surface (Munk et al. 1981
), is 420 m for each component. Incoherently adding these variances
gives rms residuals of 520 m for each component, in fair agreement with the
observed residuals. Drifters may also be entrained in Langmuir cells, often
associated with down-wind jets (Weller et al. 1985
), further increasing the residuals.
 Weak temporal modulations are in fact present in the residuals. Longitudinal and transverse correlation functions are defined as
Weak temporal modulations are in fact present in the residuals. Longitudinal and transverse correlation functions are defined as
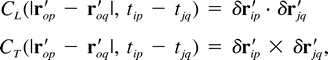
in which r op is the average position of drifter p in the frame of reference in translation, and
op is the average position of drifter p in the frame of reference in translation, and  r
r ip is the displacement of the ith position from the average. Figure A3
ip is the displacement of the ith position from the average. Figure A3  shows the temporal correlation functions normalized by CL(0, 0), for |r
shows the temporal correlation functions normalized by CL(0, 0), for |r op
op  r
r oq| < 6 km, averaged in bins of 35 products. Although the dataset is small, CT(0,
oq| < 6 km, averaged in bins of 35 products. Although the dataset is small, CT(0,  t)
nevertheless shows a striking semidiurnal modulation, corresponding to clockwise
rotation. A semidiurnal modulation is also apparent in CL(0,
t)
nevertheless shows a striking semidiurnal modulation, corresponding to clockwise
rotation. A semidiurnal modulation is also apparent in CL(0,  t), superimposed over a longer period oscillation, possibly inertial or diurnal.
t), superimposed over a longer period oscillation, possibly inertial or diurnal. This
test showed that, in a region with negligible gradients, incompletely sampled
tidal, near-inertial, and internal waves resulted in a standard error of
2
This
test showed that, in a region with negligible gradients, incompletely sampled
tidal, near-inertial, and internal waves resulted in a standard error of
2 ×
× 10
10 6 s
6 s 1
1  f/40.
The error would increase for stronger inertial oscillations, unless the sampling
scheme can resolve them. The estimation error cannot be easily decreased
by increasing the number of drifters or the tracking period, since the assumption
of a scale separation between residual motions and mesoscale flow constrains
the cluster size nL to be smaller than the internal radius of deformation,
and since the assumption that the mesoscale flow is steady forbids making
the tracking period mT much larger than 1/f. As we found in section 3, this constraint is most severe in regions subject to large horizontal straining: after a time
f/40.
The error would increase for stronger inertial oscillations, unless the sampling
scheme can resolve them. The estimation error cannot be easily decreased
by increasing the number of drifters or the tracking period, since the assumption
of a scale separation between residual motions and mesoscale flow constrains
the cluster size nL to be smaller than the internal radius of deformation,
and since the assumption that the mesoscale flow is steady forbids making
the tracking period mT much larger than 1/f. As we found in section 3, this constraint is most severe in regions subject to large horizontal straining: after a time  =
= 
 1, clusters are too elongated to provide reliable estimates of
1, clusters are too elongated to provide reliable estimates of 
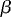 u
u
REFERENCES
Batchelor, G. K., 1967: Fluid Dynamics. Cambridge University Press 615 pp.
Bernstein, R. L., L. Breaker, and R. Whritner, 1977: California current eddy formation. Science, 195, 353–359.
Businger, J. A., and W. J. Shaw,
1984: The response of the marine boundary layer to mesoscale variations in
sea-surface temperature. Dyn. Atmos. Oceans, 8, 267–281.
Chew, F., and G. A. Berberian, 1971: A determination of horizontal divergence in the Gulf Stream off Cape Lookout. J. Phys. Oceanogr., 1, 39–44.
D’Asaro, E. A., 1985: Upper ocean
temperature structure, inertial currents and Richardson numbers observed
during strong meteorological forcing. J. Phys. Oceanogr., 15, 943–962.
Davis, R. E., 1985: Drifter observations of coastal surface currents during CODE: the method and descriptive view. J. Geophys. Res., 90, 4741–4755.
Dewey, R. K., J. N. Moum, C. A. Paulson, D. R. Caldwell, and S. D. Pierce, 1991: Structure and dynamics of a coastal filament. J. Geophys. Res., 96, 14 885–14
885–14 908.
908.
Efron, B., and G. Gong, 1983: A leisurely look at the bootstrap, the jacknife and the cross-validation. Amer. Stat., 37, 36–48.
Emery, W. J., W. G. Lee, and L. Magaard,
1984: Geographic and seasonal distributions of Brunt–Väisälä frequency and
Rossby radii in the North Pacific and North Atlantic. J. Phys. Oceanogr., 14, 294–317.
Flament, P., L. Armi, and L. Washburn, 1985: The evolving structure of an upwelling filament. J. Geophys. Res., 90, 11 765–11
765–11 778.
778.
——, J. Firing, M. Sawyer, and C.
Trefois, 1994: Amplitude and horizontal structure of a large diurnal sea
surface warming event during the Coastal Ocean Dynamics Experiment. J. Phys. Oceanog., 24, 124–139.
Hanson, H. P., 1987: Response of
marine atmospheric boundary layer height to sea-surface temperature changes:
Mixed-layer theory. J. Geophys. Res., 92, 8226–8230.
Huyer, A., and Coauthors, 1991: Currents and water masses of the coastal transition zone of northern California. J. Geophys. Res., 96, 14 809–14
809–14 832.
832.
Kirwan, A. D., 1975: Oceanic velocity gradients. J. Phys. Oceanogr., 5, 729–735.
Klein, P., and J. P. LeSaos, 1986: Influence of a quasi-geostrophic flow on the deepening of the wind-mixed layer. Geophys. Res. Lett., 13, 452–455.
Kosro, P. M., and A. Huyer, 1986: CTD and velocity surveys of seaward jets off Northern California. J. Geophys. Res., 91, 7680–7690.
——, ——, and Coauthors, 1991: The
structure of the transition zone between coastal waters and the open ocean
off northern California, winter and spring 1987. J. Geophys. Res., 96, 14 707–14
707–14 730.
730.
Kunze, E., and T. B. Sanford, 1986: Near-inertial wave interactions with mean flow and bottom topography near Caryn seamount. J. Phys. Oceanogr., 16, 109–120.
Meyer, S. L., 1975: Data Analysis for Scientists and Engineers. J. Wiley and Sons.
Molinari, R., and A. D. Kirwan,
1975: Calculations of differential kinematic properties from Lagrangian observations
in the western Caribbean Sea. J. Phys. Oceanogr., 5, 483–491.
Moum, J. N., D. J. Carlson, and T. J. Cowles, 1990: Sea slicks and surface strain. Deep-Sea Res., 37, 767–775.
Munk, W., 1981: Internal waves and small-scale processes. Evolution of Physical Oceanography, B. A. Warren and C. Wunsch, Eds., The MIT Press, 264–291.
——, F. Snodgrass, and M. Wimbush, 1970: Tides off-shore: Transition from California coastal to deep waters. Geophys. Fluid Dyn., 1, 161–235.
Niiler, P. P., 1969: On the Ekman divergence in an oceanic jet. J. Geophys. Res., 74, 7048–7051.
——, P. M. Poulain, and L. T. Haury,
1989: Synotic three-dimensional circulation in an offshore-flowing filament
of the California Current. Deep-Sea Res., 36, 385–405.
Noble, M., L. K. Rosenfeld, R. L.
Smith, J. V. Gardner, and R. C. Beardsley, 1986: Tidal currents seaward of
the Northern California continental shelf. J. Geophys. Res., 92, 1733–1744.
Okubo, A., and C. C. Ebbesmeyer,
1976: Determination of vorticity, divergence and deformation rates from analysis
of drogue observations. Deep-Sea Res., 23, 349–352.
Pollard, R. T., and R. C. Millard, 1970: Comparison between observed and simulated wind-generated inertial oscillations. Deep-Sea Res., 17, 813–821.
Reed, R. K., 1971: An observation of divergence in the Alaskan stream. J. Phys. Oceanogr., 1, 282–283.
Rienecker, M., C. N. K. Mooers,
D. E. Hagan, and A. R. Robinson, 1985: A cool anomaly off Northern California:
An investigation using IR imagery and in situ data. J. Geophys. Res., 90, 4807–4818.
Sanford, T. B., R. G. Drever, J.
H. Dunlap, M. A. Kennelly, M. D. Prater, and G. L. Welsh, 1988: The Towed
Transport Meter (TTM) and its sea test on R/V Thompson cruise 202. Applied
Physics Laboratory Rep. APL-UW 8713, University of Washington, 42 pp. [Available
from Applied Physics Laboratory, University of Washington, Seattle, WA 98105-6698.]
Sheres, D., K. E. Kenyon, R. L.
Bernstein, and R. C. Beardsley, 1985:Large horizontal velocity shears in
the ocean obtained from images of refracting swell and in-situ moored current
data. J. Geophys. Res., 90, 4943–4950.
Smith, S. D., 1988: Coefficients
for sea surface wind stress, heat flux and wind profile as a function of
wind speed and temperature. J. Geophys. Res., 93, 15 467–15
467–15 472.
472.
Stern, M. E., 1975: Ocean Circulation Physics. Academic Press.
Thorpe, S. A., 1983: Benthic observations on the Madeira abyssal plain: Fronts. J. Phys. Oceanogr., 13, 1430–1440.
Washburn, L., D., Kadko, B. H.
Jones, T. Hayward, P. M. Kosro, T. P. Santon, S. Ramp, and T. J. Cowles,
1991: Water mass subduction and the transport of phytoplankton in a coastal
upwelling system. J. Geophys. Res., 96, 14 927–14
927–14 946.
946.
Weller, R. A., J. P. Dean, J. Marra,
J. F. Price, E. A. Francis, and D. C. Boardman, 1985: Three-dimensional flow
in the upper-ocean. Science, 227, 1552–1556.
Figures

Click on thumbnail for full-sized image.
 Fig.
1. Thermal infrared images from the NOAA polar orbiting satellites: (a) 0300
UTC 9 Jul, (b) 0300 UTC 24 Jul, (c) 1000 UTC 5 Aug. Light gray shades correspond
to cold water. Surface velocities obtained by following thermal features
over an
Fig.
1. Thermal infrared images from the NOAA polar orbiting satellites: (a) 0300
UTC 9 Jul, (b) 0300 UTC 24 Jul, (c) 1000 UTC 5 Aug. Light gray shades correspond
to cold water. Surface velocities obtained by following thermal features
over an  24-h period are overlaid on (a) and (c). No sequence exists for (b). The 2000-m isobath is shown by a dashed line.
24-h period are overlaid on (a) and (c). No sequence exists for (b). The 2000-m isobath is shown by a dashed line.
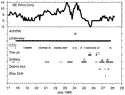
Click on thumbnail for full-sized image.
 Fig.
2. Schedule of the experiment, showing the times of cloudless satellite images,
of underway sampling of surface temperature and salinity, of the hydrographic
stations, of the tow-yo sections, of the drifters fixes, of the sightings
of the debris line, and of the ship drift study. A time series of the alongshore
(southeastward) component of the wind from the log of the R/V Sproul is also shown.
Fig.
2. Schedule of the experiment, showing the times of cloudless satellite images,
of underway sampling of surface temperature and salinity, of the hydrographic
stations, of the tow-yo sections, of the drifters fixes, of the sightings
of the debris line, and of the ship drift study. A time series of the alongshore
(southeastward) component of the wind from the log of the R/V Sproul is also shown.
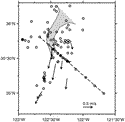
Click on thumbnail for full-sized image.
 Fig.
3. Velocity vectors from individual drifters deployments and actual positions
of the hydrographic stations. For reference, the boundaries of the cold filament
on 24 July are shown stippled. The section along the dashed line was repeated
four times during the cruise. The stations shown in Fig. 14
Fig.
3. Velocity vectors from individual drifters deployments and actual positions
of the hydrographic stations. For reference, the boundaries of the cold filament
on 24 July are shown stippled. The section along the dashed line was repeated
four times during the cruise. The stations shown in Fig. 14  are marked with a star. The positions of the drifters clusters and of the tow-yo sections are shown in Fig. 8
are marked with a star. The positions of the drifters clusters and of the tow-yo sections are shown in Fig. 8  and Fig. 15
and Fig. 15  .
.

Click on thumbnail for full-sized image.
 Fig. 4. Hydrographic section along the NW–SE line shown in Fig. 3
Fig. 4. Hydrographic section along the NW–SE line shown in Fig. 3  ,
using stations taken on 20 and 21 July: (a) surface temperature, (b) surface
salinity, (c) surface geopotential anomaly, (d) surface geostrophic velocity,
(e) contours of geostrophic velocity at 0.1 m s
,
using stations taken on 20 and 21 July: (a) surface temperature, (b) surface
salinity, (c) surface geopotential anomaly, (d) surface geostrophic velocity,
(e) contours of geostrophic velocity at 0.1 m s 1 intervals. (c), (d), (e) are referenced to 500 dbar.
1 intervals. (c), (d), (e) are referenced to 500 dbar.
Click on thumbnail for full-sized image.
 Fig.
5. Profiles of geostrophic velocity referenced to 500 dbar. Solid: between
two stations spaced 7 km apart near the axis of the jet. Dashed: between
two stations spaced 8 km apart near the axis of the jet rooted near Point
Arena in 1982 (from Flament et al. 1985
).
Fig.
5. Profiles of geostrophic velocity referenced to 500 dbar. Solid: between
two stations spaced 7 km apart near the axis of the jet. Dashed: between
two stations spaced 8 km apart near the axis of the jet rooted near Point
Arena in 1982 (from Flament et al. 1985
).
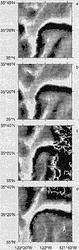
Click on thumbnail for full-sized image.
 Fig.
6. Sequence of images showing a region of cross-isotherm convergence near
the dotted line: (a) 2200 UTC 8 Jul, (b) 0300 UTC 9 Jul (also shown in Fig. 1
Fig.
6. Sequence of images showing a region of cross-isotherm convergence near
the dotted line: (a) 2200 UTC 8 Jul, (b) 0300 UTC 9 Jul (also shown in Fig. 1  ),
(c) 1500 UTC 9 Jul, (d) 0300 UTC 10 Jul. These images were enlarged and enhanced
by a high-pass filter to emphasize small thermal features.
),
(c) 1500 UTC 9 Jul, (d) 0300 UTC 10 Jul. These images were enlarged and enhanced
by a high-pass filter to emphasize small thermal features.
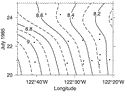
Click on thumbnail for full-sized image.
 Fig.
7. Time/longitude contour plot of geopotential anomaly along repeated section,
showing northwestward translation of the field.
Fig.
7. Time/longitude contour plot of geopotential anomaly along repeated section,
showing northwestward translation of the field.

Click on thumbnail for full-sized image.
 Fig.
8. Positions of the clusters with respect to the boundaries of the cold filament
observed in the image of 24 July, shown stippled. The positions have been
extrapolated to the time of the image to correct for the translation speed
inferred from Fig. 7
Fig.
8. Positions of the clusters with respect to the boundaries of the cold filament
observed in the image of 24 July, shown stippled. The positions have been
extrapolated to the time of the image to correct for the translation speed
inferred from Fig. 7  . The ship track used to estimate ship drift is also shown.
. The ship track used to estimate ship drift is also shown.

Click on thumbnail for full-sized image.
 Fig. 9. (a) Linearly interpolated drifters trajectories for cluster A, deployed starting 1700 UTC 26 Jul (cf. Fig. 2
Fig. 9. (a) Linearly interpolated drifters trajectories for cluster A, deployed starting 1700 UTC 26 Jul (cf. Fig. 2  ).
The distances between successive dashes in the trajectories correspond to
½ hour. The launch positions are shown as dots and the recorded positions
are shown as stars. The approximate position of the debris line relative
to the cluster is shown by a thick line. (b) Map of surface salinity sampled
while tracking this cluster, with dark gray shades representing low salinity
cold water. The north–south salinity front corresponding to the eastern boundary
of the jet is seen. The origin of the coordinates is at 35°40
).
The distances between successive dashes in the trajectories correspond to
½ hour. The launch positions are shown as dots and the recorded positions
are shown as stars. The approximate position of the debris line relative
to the cluster is shown by a thick line. (b) Map of surface salinity sampled
while tracking this cluster, with dark gray shades representing low salinity
cold water. The north–south salinity front corresponding to the eastern boundary
of the jet is seen. The origin of the coordinates is at 35°40 N, 122°28
N, 122°28 W.
W.

Click on thumbnail for full-sized image.
 Fig.
10. A panorama of photographs of the accumulation of debris taken 1530 UTC
27 Jul, viewing toward the southwest (left), west (center), and northwest
(right). The inset shows longitude of the debris line as a function of time.
Fig.
10. A panorama of photographs of the accumulation of debris taken 1530 UTC
27 Jul, viewing toward the southwest (left), west (center), and northwest
(right). The inset shows longitude of the debris line as a function of time.
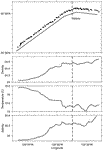
Click on thumbnail for full-sized image.
 Fig. 11. Ship track crossing the convergence zone from east to west at 1.3 m s
Fig. 11. Ship track crossing the convergence zone from east to west at 1.3 m s 1, starting 0630 UTC 27 Jul. LORAN-C positions are shown at 1-min intervals (
1, starting 0630 UTC 27 Jul. LORAN-C positions are shown at 1-min intervals ( 100
m). The latitude scale has been exaggerated by a factor of 3 to show the
southward drift of the ship entering the jet. The position of the debris
line is shown by a dashed line. Surface density, temperature, and salinity
during the crossings are shown in the lower panels.
100
m). The latitude scale has been exaggerated by a factor of 3 to show the
southward drift of the ship entering the jet. The position of the debris
line is shown by a dashed line. Surface density, temperature, and salinity
during the crossings are shown in the lower panels.

Click on thumbnail for full-sized image.
 Fig. 12. (a) Linearly interpolated drifters trajectories for cluster B,
deployed starting 0930 UTC 27 Jul. The drifters are numbered at their launch
position and the recorded positions are shown as stars. The origin of the
coordinates is at 35°37
Fig. 12. (a) Linearly interpolated drifters trajectories for cluster B,
deployed starting 0930 UTC 27 Jul. The drifters are numbered at their launch
position and the recorded positions are shown as stars. The origin of the
coordinates is at 35°37 N, 122°31
N, 122°31 W.
(b) Trajectories in the frame of reference translating with the mean flow.
The distance between successive dashes in the trajectories corresponds to
interpolated intervals of ½ hour.
W.
(b) Trajectories in the frame of reference translating with the mean flow.
The distance between successive dashes in the trajectories corresponds to
interpolated intervals of ½ hour.
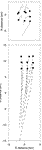
Click on thumbnail for full-sized image.
 Fig. 13. Same as Fig. 12
Fig. 13. Same as Fig. 12  but for cluster C, deployed starting 1930 UTC 24 Jul. The origin of the coordinates is at 35°56
but for cluster C, deployed starting 1930 UTC 24 Jul. The origin of the coordinates is at 35°56 N, 122°32
N, 122°32 W.
W.
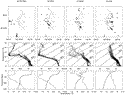
Click on thumbnail for full-sized image.
 Fig. 14. Aggregate T–S
diagrams for the four water column types identified: (a) “Far West” of the
filament, (b) “West” of the front, (c) “Mixed” mixing region near the front,
(d) “East” of the front. The top panel shows the position of the stations
used for each type. The bottom panel shows vertical profiles of temperature
and salinity for a typical station in each type, marked by a star in the
top panel (see also Figs. 3
Fig. 14. Aggregate T–S
diagrams for the four water column types identified: (a) “Far West” of the
filament, (b) “West” of the front, (c) “Mixed” mixing region near the front,
(d) “East” of the front. The top panel shows the position of the stations
used for each type. The bottom panel shows vertical profiles of temperature
and salinity for a typical station in each type, marked by a star in the
top panel (see also Figs. 3  and 15
and 15  for the location of these stations).
for the location of these stations).
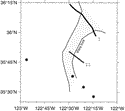
Click on thumbnail for full-sized image.
 Fig. 15. Positions of the tow-yo sections and of the four CTD stations shown in Fig. 14
Fig. 15. Positions of the tow-yo sections and of the four CTD stations shown in Fig. 14  with respect to the boundaries of the cold filament observed in the image
of 24 Jul. The positions of the sections have been extrapolated to the time
of the image to correct for the translation speed inferred from Fig. 7
with respect to the boundaries of the cold filament observed in the image
of 24 Jul. The positions of the sections have been extrapolated to the time
of the image to correct for the translation speed inferred from Fig. 7  .
.

Click on thumbnail for full-sized image.
 Fig. 16. Tow-yo sections of temperature (top) and salinity (bottom) vs pressure across the filament. Left panels: tow-yo I; right panels: tow-yo II. The depth/distance path of the undulating CTD is shown above each section. The isopycnals are overlaid.
Fig. 16. Tow-yo sections of temperature (top) and salinity (bottom) vs pressure across the filament. Left panels: tow-yo I; right panels: tow-yo II. The depth/distance path of the undulating CTD is shown above each section. The isopycnals are overlaid.
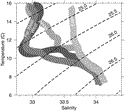
Click on thumbnail for full-sized image.
 Fig. 17. Summary of the four basic water column types, shown as the isopycnal-averaged T–S diagram of each type (see text).
Fig. 17. Summary of the four basic water column types, shown as the isopycnal-averaged T–S diagram of each type (see text).

Click on thumbnail for full-sized image.
 Fig. A1. Drifters tracking schedule. The origin of time is set at the start of the deployment, 1820 UTC 11 Aug.
Fig. A1. Drifters tracking schedule. The origin of time is set at the start of the deployment, 1820 UTC 11 Aug.

Click on thumbnail for full-sized image.
 Fig.
A2. (a) Linearly interpolated trajectories, dashed every hour. The deployment
configuration of the cluster is outlined. The origin of coordinates is set
at 36°10
Fig.
A2. (a) Linearly interpolated trajectories, dashed every hour. The deployment
configuration of the cluster is outlined. The origin of coordinates is set
at 36°10 N, 122°36
N, 122°36 W.
(b) Residual trajectories dashed every hour, after removing the mean translation.
The start of each track is marked by a star. The radii of the concentric
circles represent the 750-m rms residual displacement and the 100-m rms LORAN-C
error.
W.
(b) Residual trajectories dashed every hour, after removing the mean translation.
The start of each track is marked by a star. The radii of the concentric
circles represent the 750-m rms residual displacement and the 100-m rms LORAN-C
error.
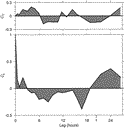
Click on thumbnail for full-sized image.
 Fig. A3. (a) Temporal longitudinal coherence function CL(
Fig. A3. (a) Temporal longitudinal coherence function CL( r < 6 km,
r < 6 km,  t); (b) temporal transverse coherence function CT(
t); (b) temporal transverse coherence function CT( r < 6 km,
r < 6 km,  t). Here, f indicates the inertial period.
t). Here, f indicates the inertial period.
 *
* School of Ocean and Earth Sciences and Technology, University of Hawaii Contribution Number 4898.
School of Ocean and Earth Sciences and Technology, University of Hawaii Contribution Number 4898.
 Corresponding author address: Dr. Pierre Flament, Department of Oceanography, University of Hawaii, 1000 Pope Rd., Honolulu, HI 96822.
Corresponding author address: Dr. Pierre Flament, Department of Oceanography, University of Hawaii, 1000 Pope Rd., Honolulu, HI 96822.
 E-mail: pflament@hawaii.edu
E-mail: pflament@hawaii.edu
Tables
 Table 1. Flow parameters.
Table 1. Flow parameters.
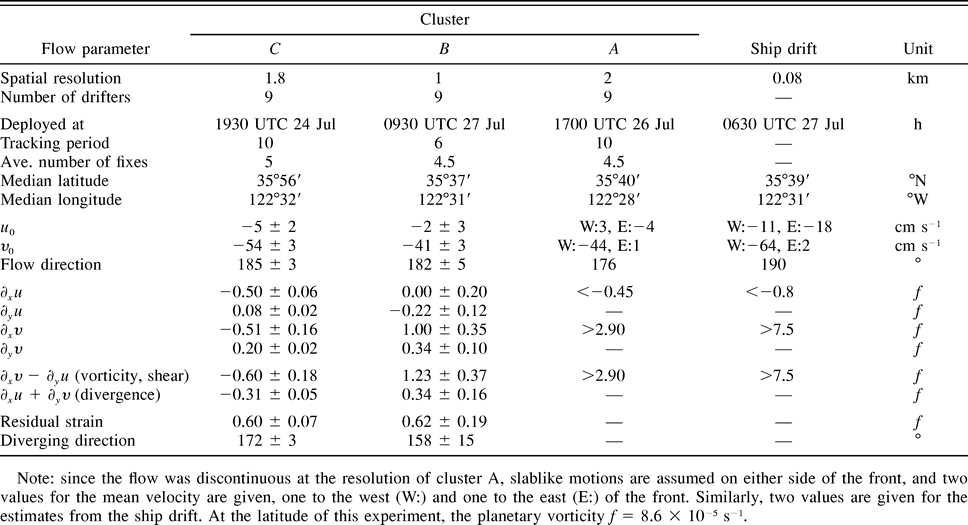
 Table A1. Flow parameters.
Table A1. Flow parameters.
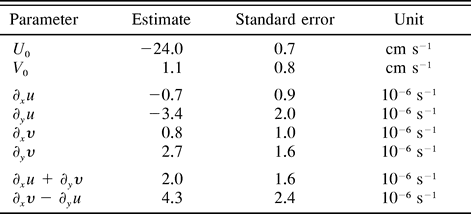
![]() With
the objective of measuring convergence directly to confirm previous observations
of frontal subduction, a seaward upwelling jet off central California was
studied using satellite infrared images, hydrographic sections, ship drift,
and clusters of surface drifters. The cyclonic front of the jet was sharper
than 1 km, resulting in a shear several times larger than f. A cross-frontal convergence of 7 cm s
With
the objective of measuring convergence directly to confirm previous observations
of frontal subduction, a seaward upwelling jet off central California was
studied using satellite infrared images, hydrographic sections, ship drift,
and clusters of surface drifters. The cyclonic front of the jet was sharper
than 1 km, resulting in a shear several times larger than f. A cross-frontal convergence of 7 cm s 1 over the width of the front (equivalent to 0.8f)
was visible as a 20-m-wide accumulation of debris. The sharpness of the front
lasted at least for a day. Away from the cyclonic front, the divergence of
the flow was small and the shear was less than 0.6f. Thermohaline
layers, originating at the front, were interleaving along isopycnals, suggesting
water subduction. It is proposed that the asymetry between anticyclonic and
cyclonic sides of the jet, and the strong convergence at the cyclonicfront,
resulted from a frictionally driven ageostrophic secondary circulation superimposed
on the geostrophic flow.
1 over the width of the front (equivalent to 0.8f)
was visible as a 20-m-wide accumulation of debris. The sharpness of the front
lasted at least for a day. Away from the cyclonic front, the divergence of
the flow was small and the shear was less than 0.6f. Thermohaline
layers, originating at the front, were interleaving along isopycnals, suggesting
water subduction. It is proposed that the asymetry between anticyclonic and
cyclonic sides of the jet, and the strong convergence at the cyclonicfront,
resulted from a frictionally driven ageostrophic secondary circulation superimposed
on the geostrophic flow. ·
· N,
122°W), which was surveyed between 17 and 29 July 1985. The mesoscale structure
of the filament, inferred from hydrographic stations, underway surface temperature
and salinity, and drifters tracks, is presented in
N,
122°W), which was surveyed between 17 and 29 July 1985. The mesoscale structure
of the filament, inferred from hydrographic stations, underway surface temperature
and salinity, and drifters tracks, is presented in 
 30 km and its geostrophic transport referenced to 500 dbar was 2.0
30 km and its geostrophic transport referenced to 500 dbar was 2.0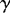 t, s being a cross-isotherm coordinate, a rough estimate of the convergence rate is
t, s being a cross-isotherm coordinate, a rough estimate of the convergence rate is 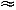 1.2
1.2 x
x across the front was larger than
across the front was larger than 
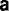 (r
(r  (1)
(1)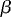 u
u is the second-order velocity gradient tensor. The drifter trajectories for clusters B and C are shown in Figs. 12
is the second-order velocity gradient tensor. The drifter trajectories for clusters B and C are shown in Figs. 12 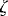
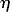
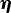 ) and a nondivergent strain,
) and a nondivergent strain, 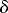
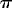 /7.5f
= 2.7 h). The asymmetry between the cyclonic and anticyclonic sides of the
jet and the very large cyclonic shears are consistent with the findings of
/7.5f
= 2.7 h). The asymmetry between the cyclonic and anticyclonic sides of the
jet and the very large cyclonic shears are consistent with the findings of
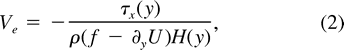
 , U, or H induce variations of Ve, thus Ekman convergence/divergence. Specifically:
, U, or H induce variations of Ve, thus Ekman convergence/divergence. Specifically:

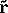 ip = (rip + ri+1p)/2 is the mean position of the drifter during that interval.
ip = (rip + ri+1p)/2 is the mean position of the drifter during that interval.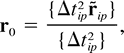
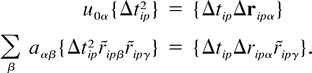
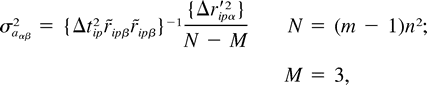
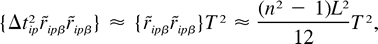
 a
a